
【题目】在平面直角坐标系xOy中![]() 如图
如图![]() ,已知抛物线
,已知抛物线![]() ,经过点
,经过点![]() 、
、![]() .
.
(1)求此抛物线顶点C的坐标;
(2)联结AC交y轴于点D,联结BD、BC,过点C作![]() ,垂足为点H,抛物线对称轴交x轴于G,联结HG,求HG的长.
,垂足为点H,抛物线对称轴交x轴于G,联结HG,求HG的长.

【答案】(1)C(2,-3);(2)![]() .
.
【解析】试题分析:(1)已知抛物线过A,B两点,可将A,B的坐标代入抛物线的解析式中用待定系数法即可求出抛物线的解析式.然后可根据抛物线的解析式得出顶点C的坐标.
(2)分别求直线AC的解析式和BD的解析式,直线AC:y=-x-1,直线BD:y=![]() x-1,可得D和P的坐标,证明△BPG∽△CPH和△HPG∽△CPB,列比例式可得HG的长
x-1,可得D和P的坐标,证明△BPG∽△CPH和△HPG∽△CPB,列比例式可得HG的长
试题解析:(1)把A(-1,0)、B(5,0)代入抛物线解析式,
得: 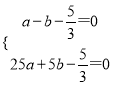 ,
,
解得: 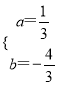 ,
,
∴抛物线的解析式为:y=![]() x2
x2![]() x
x![]() =
=![]() (x2)23,
(x2)23,
∴顶点C(2,-3)
(2)设BD与CG相交于点P,

设直线AC的解析式为:y=kx+b
把A(-1,0)和C(2,-3)代入得:
![]() ,
,
解得: ![]()
则直线AC:y=-x-1,
∴D(0,-1),
同理可得直线BD:y=![]() x-1,
x-1,
∴P(2,![]() )
)
∵∠CHP=∠PGB=90°,∠GPB=∠CPH
∴△BPG∽△CPH,
∴![]() ,
,
∴△HPG∽△CPB,
∴![]() ,
,
∴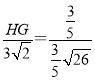 ,
,
∴HG=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,F是AD的中点,延长BC到点E,使CE=![]() BC,连接DE,CF.
BC,连接DE,CF.
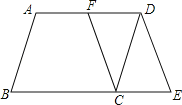
(1)求证:四边形CEDF是平行四边形;
(2)若AB=4,AD=10,∠B=60°,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,图形
中,图形![]() 的投影矩形定义如下:矩形的两组对边分别平行于
的投影矩形定义如下:矩形的两组对边分别平行于![]() 轴,
轴,![]() 轴,图形
轴,图形![]() 的顶点在矩形的边上或内部,且矩形的面积最小.设矩形的较长的边与较短的边的比为
的顶点在矩形的边上或内部,且矩形的面积最小.设矩形的较长的边与较短的边的比为![]() ,我们称常数
,我们称常数![]() 为图形
为图形![]() 的投影比,如图1,矩形
的投影比,如图1,矩形![]() 为
为![]() 的投影矩形,其投影比
的投影矩形,其投影比![]() .
.
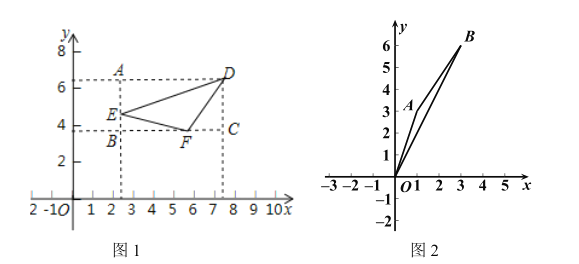
(1)如图2,若点![]() ,则
,则![]() 投影比
投影比![]() 的值为________________;
的值为________________;
(2)已知点![]() ,点
,点![]() ,且
,且![]() 投影比
投影比![]() ,则
,则![]() 点坐标可能是__________(填写序号);
点坐标可能是__________(填写序号);
①![]() ②
②![]() ③
③![]() ④
④![]()
(3)已知点![]() ,在直线
,在直线![]() 上有一点
上有一点![]() 和一动点
和一动点![]() ,且
,且![]() ,是否存在这样的
,是否存在这样的![]() ,使得
,使得![]() 的投影比
的投影比![]() 为定值?若存在,请求出
为定值?若存在,请求出![]() 的范围及定值
的范围及定值![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题:
![]() 若
若![]() ,则
,则![]() ;
;
![]() 若
若![]() ,则一元二次方程
,则一元二次方程![]() 有两个不相等的实数根;
有两个不相等的实数根;
![]() 若
若![]() ,则一元二次方程
,则一元二次方程![]() 有两个不相等的实数根;
有两个不相等的实数根;
![]() 若
若![]() ,则二次函数
,则二次函数![]() 的图象与坐标轴的公共点的个数是2或3.
的图象与坐标轴的公共点的个数是2或3.
其中正确的是![]()
A. 只有![]() B. 只有
B. 只有![]() C. 只有
C. 只有![]() D. 只有
D. 只有![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学校组织的以”垃圾分类 从我做起“的主题知识竞赛活动中,王老师随机抽取了班中参赛的6名学生成绩,若以80分为标准,超过这个分数用正数表示,不足的分数用负数表示,成绩记录如下:-3,+7,-12,+6 , -21 ,+14
(1) 最高分比最低分多多少分?这6名学生平均每人得多少分?
(2) 若规定:成绩高于80分的学生操行分每人加3分,成绩在60~80分的学生操行分每人加2分,成绩在60分以下的学生操行分每人扣1分,那么这6名学生共加操行分多少分?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=![]() AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①△ABE≌△ADH;②HE=CE;③H是BF的中点;④AB=HF;其中正确的有( )
AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①△ABE≌△ADH;②HE=CE;③H是BF的中点;④AB=HF;其中正确的有( )
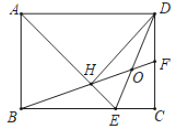
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周长相等的正三角形、正四边形、正六边形的面积S3、S4、S6间的大小关系是( )
A. S3>S4>S6 B. S6>S4>S3 C. S6>S3>S4 D. S4>S6>S3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com