
【题目】如图,已知⊙O的直径AB=12,弦AC=10,D是弧BC的中点,过点D作DE⊥AC,交AC的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)求AE的长.

【答案】(1)见解析;(2)11.
【解析】分析:(1)连接OD,由D为弧BC的中点,得到两条弧相等,进而得到两个同位角相等,确定出OD与AE平行,利用两直线平行同旁内角互补得到OD与DE垂直,即可得证;
(2)过O作OF垂直于AC,利用垂径定理得到F为AC中点,再由四边形OFED为矩形,求出FE的长,由AF+EF求出AE的长即可.
详解:(1)连接OD,
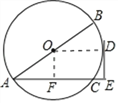
∵D为弧BC的中点,∴弧BD=弧CD,
∴∠BOD=∠BAE,∴OD∥AE,
∵DE⊥AC,∴∠ADE=90°,∴∠AED=90°,
∴OD⊥DE,
则DE为圆O的切线;
(2)过点O作OF⊥AC,
∵AC=10,∴AF=CF=![]() AC=5,
AC=5,
∵∠OFE=∠DEF=∠ODE=90°,
∴四边形OFED为矩形,
∴FE=OD=![]() AB,
AB,
∵AB=12,∴FE=6,
则AE=AF+FE=5+6=11.


科目:初中数学 来源: 题型:
【题目】数学问题:用边长相等的正三角形、正方形和正六边形能否进行平面图形的镶嵌?
问题探究:为了解决上述数学问题,我们采用分类讨论的思想方法去进行探究.
探究一:从正三角形、正方形和正六边形中任选一种图形,能否进行平面图形的镶嵌?
第一类:选正三角形.因为正三角形的每一个内角是60°,所以在镶嵌平面时,围绕某一点有6个正三角形的内角可以拼成一个周角,所以用正三角形可以进行平面图形的镶嵌.
第二类:选正方形.因为正方形的每一个内角是90°,所以在镶嵌平面时,围绕某一点有4个正方形的内角可以拼成一个周角,所以用正方形也可以进行平面图形的镶嵌.
第三类:选正六边形.(仿照上述方法,写出探究过程及结论)
探究二:从正三角形、正方形和正六边形中任选两种图形,能否进行平面图形的镶嵌?
第四类:选正三角形和正方形
在镶嵌平面时,设围绕某一点有x个正三角形和y个正方形的内角可以拼成个周角.根据题意,可得方程
60x+90y=360
整理,得2x+3y=12.
我们可以找到唯一组适合方程的正整数解为![]() .
.
镶嵌平面时,在一个顶点周围围绕着3个正三角形和2个正方形的内角可以拼成一个周角,所以用正三角形和正方形可以进行平面镶嵌
第五类:选正三角形和正六边形.(仿照上述方法,写出探究过程及结论)
第六类:选正方形和正六边形,(不写探究过程,只写出结论)
探究三:用正三角形、正方形和正六边形三种图形是否可以镶嵌平面?
第七类:选正三角形、正方形和正六边形三种图形.(不写探究过程,只写结论),
查看答案和解析>>
科目:初中数学 来源: 题型:
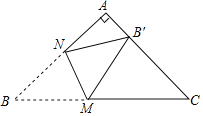
【题目】如图,在Rt△ABC中,∠A=90°,AB=AC,BC=![]() +1,点M,N分别是边BC,AB上的动点,沿MN所在的直线折叠∠B,使点B的对应点B′始终落在边AC上,若△MB′C为直角三角形,则BM的长为_______.
+1,点M,N分别是边BC,AB上的动点,沿MN所在的直线折叠∠B,使点B的对应点B′始终落在边AC上,若△MB′C为直角三角形,则BM的长为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某天一个巡警骑摩托车在一条南北大道上巡逻,他从岗亭出发,规定岗亭为原点,向北为正,这段时间行驶记录如下(单位:千米) +10,-9,+7,-15,+6,-14,+4,-2
(1)最后停留的地方在岗亭的哪个方向?距离岗亭多远?
(2)若摩托车行驶,每千米耗油0.06升,每升6.2元,且最后返回岗亭,这一天耗油共需多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
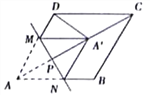
【题目】菱形ABCD的边长是4,∠DAB=60,点M,N分别在边AD,AB上,MN⊥AC,垂足为P,把△AMN沿MN折叠得到△A'MN,若△A'DC恰为等腰三角形,则AP的长为_____。
查看答案和解析>>
科目:初中数学 来源: 题型:
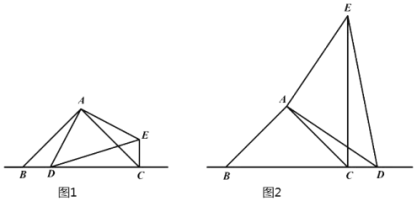
【题目】已知:△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点D是等腰直角三角形ABC斜边BC所在直线上一点(不与点B重合).
(1)如图1,当点D在线段BC上时,线段CE、BD之间的位置关系是__________,数量关系是___________;
(2)如图2,当点D在线段BC的延长线上时,探索AD、BD、CD三条线段之间的数量关系,写出结论并证明;
(3)若BD=![]() CD,直接写出∠BAD的度数。
CD,直接写出∠BAD的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
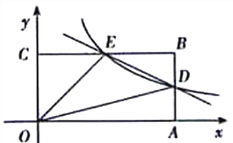
【题目】如图,在平面直角坐标系中,原点O是矩形OABC的一个顶点,点A、C都
在坐标轴上,点B的坐标是(4.2),反比例函数![]() 与AB,BC分别交于点D,E。
与AB,BC分别交于点D,E。
(1)求直线DE的解析式;
(2)若点F为y轴上一点,△OEF和△ODE的面积相等,求点F的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为打造引江枢纽风光带,一段长为1.2千米的河道整治任务交由甲、乙两个工程队接力完成,共用时60天. 已知甲队每天整治24米,乙队每天整治16米.
(1)根据题意,小明、小丽分别列出如下的一元一次方程(尚不完整): 小明:![]() . 小丽:
. 小丽:![]() =60. 请分别指出上述方程中
=60. 请分别指出上述方程中![]() 的意义,并补全方程: 小明:
的意义,并补全方程: 小明:![]() 表示 . 小丽:
表示 . 小丽:![]() 表示 .
表示 .
(2)请选择其中一种方法,求甲、乙两队分别整治河道多少米?(写出完整的解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】考试前夕,为“连粽连中”的吉祥寓意,某校食堂购进甲、乙两种粽子520个,其中甲种粽子花费600元,乙种粽子花费800元,已知甲种粽子单价比乙种粽子单价高20%,乙种粽子的单价是多少元?甲、乙两种粽子各购买了多少个?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com