
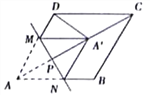
【题目】菱形ABCD的边长是4,∠DAB=60,点M,N分别在边AD,AB上,MN⊥AC,垂足为P,把△AMN沿MN折叠得到△A'MN,若△A'DC恰为等腰三角形,则AP的长为_____。
科目:初中数学 来源: 题型:
【题目】某中学库存若干套桌凳,准备修理后支援贫困山区学校,现有甲、乙两木工组,甲每天修桌凳20套,乙每天修桌凳比甲多5套,甲单独修完这些桌凳比乙单独修完多用9天,学校每天付甲组80元修理费,付乙组110元修理费.
(1)问该中学库存多少套桌凳?
(2)在修理过程中,学校要派一名工人进行质量监督,学校负担他每天10元生活补助费,现有三种修理方案:①由甲单独修理;②由乙单独修理;③甲、乙合作同时修理.你认为哪种方案省时又省钱为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,BE平分∠ABC,D是边AB上一点,以BD为直径的⊙O经过点E,且交BC于点F.
(1)求证:AC是⊙O的切线;
(2)若BF=6,⊙O的半径为5,求CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,AB=8,点P在边CD上,tan∠PBC=![]() ,点Q是在射线BP上的一个动点,过点Q作AB的平行线交射线AD于点M,点R在射线AD上,使RQ始终与直线BP垂直.
,点Q是在射线BP上的一个动点,过点Q作AB的平行线交射线AD于点M,点R在射线AD上,使RQ始终与直线BP垂直.
(1)如图1,当点R与点D重合时,求PQ的长;
(2)如图2,试探索: ![]() 的比值是否随点Q的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;
的比值是否随点Q的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;
(3)如图3,若点Q在线段BP上,设PQ=x,RM=y,求y关于x的函数关系式,并写出它的定义域.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O的直径AB=12,弦AC=10,D是弧BC的中点,过点D作DE⊥AC,交AC的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数y=![]() 的图上象有三个点(2,y1),(3,y2),(﹣1,y3),则y1,y2,y3的大小关系是( )
的图上象有三个点(2,y1),(3,y2),(﹣1,y3),则y1,y2,y3的大小关系是( )
A. y1>y2>y3B. y2>y1>y3C. y3>y1>y2D. y3>y2>y1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正n边形的周长为60,边长为a
(1)当n=3时,请直接写出a的值;
(2)把正n边形的周长与边数同时增加7后,假设得到的仍是正多边形,它的边数为n+7,周长为67,边长为b.有人分别取n等于3,20,120,再求出相应的a与b,然后断言:“无论n取任何大于2的正整数,a与b一定不相等.”你认为这种说法对吗?若不对,请求出不符合这一说法的n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】画出直线![]() 的图象,并解答下列问题:
的图象,并解答下列问题:
(1)设它的图象与y轴、x轴分别交于点A、B,求AB的长;
(2)求![]() 的周长(O为坐标原点);
的周长(O为坐标原点);
(3)求点O到直线AB的距离;
(4)求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com