
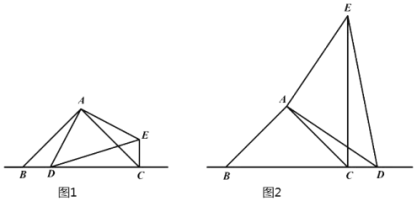
【题目】已知:△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点D是等腰直角三角形ABC斜边BC所在直线上一点(不与点B重合).
(1)如图1,当点D在线段BC上时,线段CE、BD之间的位置关系是__________,数量关系是___________;
(2)如图2,当点D在线段BC的延长线上时,探索AD、BD、CD三条线段之间的数量关系,写出结论并证明;
(3)若BD=![]() CD,直接写出∠BAD的度数。
CD,直接写出∠BAD的度数。
【答案】(1)CE⊥BD,CE=BD.(2)2AD2=CE2+CE2.(3)当D点在线段BC上时,∠BAD=60°;当D点在BC延长线上时,∠BAD=120°.
【解析】
(1)根据等腰直角三角形的性质可得∠ABC=∠ACB=45°,再根据旋转性质可得AD=AE,∠DAE=90°,然后利用同角的余角相等求出∠BAD=∠CAE,然后利用“边角边”证明△BAD和△CEF全等,从而得证;
(2)将线段AD绕点A逆时针方向旋转90°得到线段AE,连接CE.与(1)同理可得CE=BD,CE⊥BD,根据勾股定理即可求得2AD2=BD2+CD2;
(3)分两种情况分别讨论即可求得.
(1)如图1,
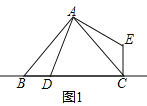
∵∠BAC=90°,AB=AC,
∴∠ABC=∠ACB=45°,
∵∠DAE=90°,
∴∠DAE=∠CAE+∠DAC=90°,
∵∠BAC=∠BAD+∠DAC=90°,
∴∠BAD=∠CAE,
在△BAD和△CAE中,
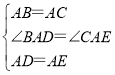 ,
,
∴△BAD≌△CAE(SAS),
∴BD=CE,∠ACE=∠ABC=45°.
∴∠BCE=∠ACB+∠ACE=90°,
∴BD⊥CE;
(2)2AD2=BD2+CD2,
理由:如图2,将线段AD绕点A逆时针方向旋转90°得到线段AE,连接CE、DE.
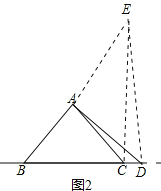
与(1)同理可证CE=BD,CE⊥BD,
∵∠EAD=90°AE=AD,
∴ED=![]() AD,
AD,
在RT△ECD中,ED2=CE2+CD2,
∴2AD2=BD2+CD2.
(3)如图3,①当D在BC边上时,将线段AD1绕点A顺时针方向旋转90°得到线段AE,连接BE,
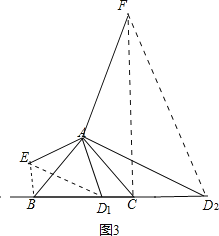
与(1)同理可证△ABE≌△ACD1,
∴BE=CD1,BE⊥BC,
∵BD=![]() CD,
CD,
∴BD1=![]() BE,
BE,
∴tan∠BD1E=![]() ,
,
∴∠BD1E=30°,
∵∠EAD1=∠EBD1=90°,
∴四边形A、D1、B、E四点共圆,
∴∠EAB=∠BD1E=30°,
∴∠BAD1=90°-30°=60°;
②当D在BC延长线上时,将线段AD绕点A逆时针方向旋转90°得到线段AF,连接CF.
同理可证:∠CFD2=30°,
∵∠FAD2=∠FCD2=90°,
∴四边形A、F、D2、C四点共圆,
∴∠CAD2=∠CFD2=30°,
∴∠BAD2=90°+30°=120°,
综上,∠BAD的度数为60°或120°.


 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:初中数学 来源: 题型:
【题目】如图,在射线OM上有三点A、B、C,满足OA=20cm,AB=60cm,BC=10cm(如图所示),点P从点O出发,沿OM方向以3cm/s的速度匀速运动,点Q从点C出发在线段CO上向点O匀速运动(点Q运动到点O时停止运动),两点同时出发.
(1)当P在线段AB上时,且PA=2PB,点Q运动到的位置恰好是线段AP的中点,求点Q的运动速度.
(2)若点Q运动速度为5cm/s,经过多长时间P、Q两点相距70cm.
(3)当点P运动到线段AB上时,分别取OP和OC的中点E、F,求![]() 的值.
的值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某油箱容量为60 L的汽车,加满汽油后行驶了100 Km时,油箱中的汽油大约消耗了![]() ,如果加满汽油后汽车行驶的路程为x Km,邮箱中剩油量为y L,则y与x之间的函数解析式和自变量取值范围分别是( )
,如果加满汽油后汽车行驶的路程为x Km,邮箱中剩油量为y L,则y与x之间的函数解析式和自变量取值范围分别是( )
A. y=0.12x,x>0 B. y=60﹣0.12x,x>0 C. y=0.12x,0≤x≤500 D. y=60﹣0.12x,0≤x≤500
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,点E,F分别在BC,AD上,且BE:EC=2:1,EF∥CD,交对角线AC于点G,则![]() _____________。
_____________。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O的直径AB=12,弦AC=10,D是弧BC的中点,过点D作DE⊥AC,交AC的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次越野赛跑中,当小明跑了1600m时,小刚跑了1450m,此后两人分别调整速度,并以各自新的速度匀速跑,又过100s时小刚追上小明,200s时小刚到达终点,300s时小明到达终点.他们赛跑使用时间t(s)及所跑距离如图s(m),这次越野赛的赛跑全程为 m?
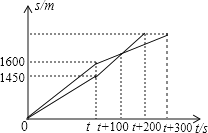
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】寻找公式,求代数式的值:从2开始,连续的偶数相加,它们的和的情况如下表:

(1)2+4+6+8+10+12=__________ (乘积的形式)
(2)当n个最小的连续偶数相加时,它们的和S与n之间有什么样的关系,用公式表示出来;
(3)并按此规律计算:(a)2+4+6+…+300的值; (b)172+174+176+…+500的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年8月连淮扬镇铁路正式通车,高邮迈入高铁时代,动车的平均速度为![]() (动车的长度不计),高铁的平均速度为
(动车的长度不计),高铁的平均速度为![]() (高铁的长度不计),扬州市内依次设有6个站点,宝应站、高邮北站、高邮高铁站、邵伯站、江都站、扬州高铁站,假设每两个相邻站点之间的路程都相等,已知一列动车、一列高铁同时经过宝应站开往扬州高铁站,若中途不停靠任何站点,到达扬州高铁站时高铁比动车将早到10分钟
(高铁的长度不计),扬州市内依次设有6个站点,宝应站、高邮北站、高邮高铁站、邵伯站、江都站、扬州高铁站,假设每两个相邻站点之间的路程都相等,已知一列动车、一列高铁同时经过宝应站开往扬州高铁站,若中途不停靠任何站点,到达扬州高铁站时高铁比动车将早到10分钟
(1)求宝应站到扬州高铁站的路程;
(2)若一列动车6:00从宝应站出发,每个站点都停靠4分钟,一列高铁6:18从宝应站出发,只停靠高邮北站、江都站,每个站点都停靠4分钟.
①求高铁经过多长时间追上动车;
②求高铁经过多长时间后,与动车的距离相距20千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园安全”受到全社会的广泛关注,某校政教处对部分学生及家长就校园安全知识的了解程度进行了随机抽样调查,并绘制成如图所示的两幅统计图,请根据统计图中的信息,解答下列问题:
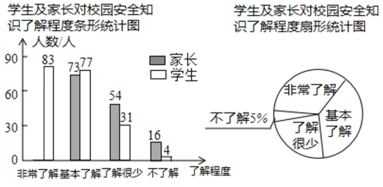
![]() 参与调查的学生及家长共有 人;
参与调查的学生及家长共有 人;
![]() 在扇形统计图中,求“基本了解"所对应的扇形的圆心角的度数;
在扇形统计图中,求“基本了解"所对应的扇形的圆心角的度数;
![]() 在条形统计图中,“非常了解”所对应的学生人数是______人 并补全条形统计图.
在条形统计图中,“非常了解”所对应的学生人数是______人 并补全条形统计图.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com