
【题目】寻找公式,求代数式的值:从2开始,连续的偶数相加,它们的和的情况如下表:

(1)2+4+6+8+10+12=__________ (乘积的形式)
(2)当n个最小的连续偶数相加时,它们的和S与n之间有什么样的关系,用公式表示出来;
(3)并按此规律计算:(a)2+4+6+…+300的值; (b)172+174+176+…+500的值.
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,A、B为x轴上两点,C、D为y轴上的两点,经过点A、C、B的抛物线的一部分c1与经过点A、D、B的抛物线的一部分c2组合成一条封闭曲线,我们把这条封闭曲线成为“蛋线”.已知点C的坐标为(0,﹣![]() ),点M是抛物线C2:y=mx2﹣2mx﹣3m(m<0)的顶点.
),点M是抛物线C2:y=mx2﹣2mx﹣3m(m<0)的顶点.
(1)求A、B两点的坐标;
(2)“蛋线”在第四象限上是否存在一点P,使得△PBC的面积最大?若存在,求出△PBC面积的最大值;若不存在,请说明理由;
(3)当△BDM为直角三角形时,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某天一个巡警骑摩托车在一条南北大道上巡逻,他从岗亭出发,规定岗亭为原点,向北为正,这段时间行驶记录如下(单位:千米) +10,-9,+7,-15,+6,-14,+4,-2
(1)最后停留的地方在岗亭的哪个方向?距离岗亭多远?
(2)若摩托车行驶,每千米耗油0.06升,每升6.2元,且最后返回岗亭,这一天耗油共需多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
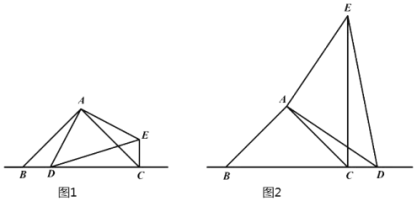
【题目】已知:△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点D是等腰直角三角形ABC斜边BC所在直线上一点(不与点B重合).
(1)如图1,当点D在线段BC上时,线段CE、BD之间的位置关系是__________,数量关系是___________;
(2)如图2,当点D在线段BC的延长线上时,探索AD、BD、CD三条线段之间的数量关系,写出结论并证明;
(3)若BD=![]() CD,直接写出∠BAD的度数。
CD,直接写出∠BAD的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
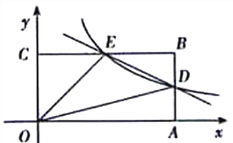
【题目】如图,在平面直角坐标系中,原点O是矩形OABC的一个顶点,点A、C都
在坐标轴上,点B的坐标是(4.2),反比例函数![]() 与AB,BC分别交于点D,E。
与AB,BC分别交于点D,E。
(1)求直线DE的解析式;
(2)若点F为y轴上一点,△OEF和△ODE的面积相等,求点F的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
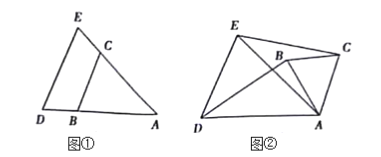
【题目】如图①,在△ABC与△ADE中,AB=AC,AD=AE,∠A是公共角。
(1)BD与CE的数量关系是:BD______CE;
(2)把图①△ABC绕点A旋转一定的角度,得到如图②所示的图形。
①求证:BD=CE;
②BD与CE所在直线的夹角与∠DAE的数量关系是什么?说明理由。
(3)若AD=10,AB=6,把图①中的△ABC绕点A顺时针旋转α度(0°<α≤360)直接写出BD长度的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为打造引江枢纽风光带,一段长为1.2千米的河道整治任务交由甲、乙两个工程队接力完成,共用时60天. 已知甲队每天整治24米,乙队每天整治16米.
(1)根据题意,小明、小丽分别列出如下的一元一次方程(尚不完整): 小明:![]() . 小丽:
. 小丽:![]() =60. 请分别指出上述方程中
=60. 请分别指出上述方程中![]() 的意义,并补全方程: 小明:
的意义,并补全方程: 小明:![]() 表示 . 小丽:
表示 . 小丽:![]() 表示 .
表示 .
(2)请选择其中一种方法,求甲、乙两队分别整治河道多少米?(写出完整的解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:我们知道a的几何意义是在数轴上数a对应的点与原点的距离.数轴上数a与数0对应点之间的距离,![]() 这 个结论可以推广为: |a- b|均表示在数轴上数a与b对应点之间的距离,例:已知|a-1|=2, 求a的值.
这 个结论可以推广为: |a- b|均表示在数轴上数a与b对应点之间的距离,例:已知|a-1|=2, 求a的值.
解:在数轴上与1的距离为2点的对应数为3和-1,即a的值为3和-1.
仿照阅读材料的解法,解决下列问题
(1)已知![]() ,求a的值.
,求a的值.
(2)若数轴上表示a的点在-4与2之间,则|a+4|+|a-2|的值为___
(3)当a满足什么条件时,|a-1|+ |a+2|有最小值,最小值是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com