
【题目】如图,在射线OM上有三点A、B、C,满足OA=20cm,AB=60cm,BC=10cm(如图所示),点P从点O出发,沿OM方向以3cm/s的速度匀速运动,点Q从点C出发在线段CO上向点O匀速运动(点Q运动到点O时停止运动),两点同时出发.
(1)当P在线段AB上时,且PA=2PB,点Q运动到的位置恰好是线段AP的中点,求点Q的运动速度.
(2)若点Q运动速度为5cm/s,经过多长时间P、Q两点相距70cm.
(3)当点P运动到线段AB上时,分别取OP和OC的中点E、F,求![]() 的值.
的值.
![]()
【答案】(1)![]() cm/s(2)经过
cm/s(2)经过![]() 秒或
秒或![]() 秒两点相距70cm(3)2
秒两点相距70cm(3)2
【解析】
此题较为复杂,但读懂了题意根据速度公式就可求解.
(1)从题中我们可以看出点P及Q是运动的,当PA=2PB时实际上是P正好到了AB的三等分点上,而且PA=40, PB=20.由速度公式就可求出P点的运动时间,也是点Q的运动时间,点Q运动到的位置恰好是线段AP的中点,由此就可求出CQ长和点Q的速度.
(2)若点Q运动速度为5cm/s,经过多长时间P、Q两点相距70cm,这也有两种情况即当它们相向而行时,和它们背向而行时,此题可设运动时间为t秒,列方程就可解了.
(3) 此题就可把它当成一个静止的线段问题来解决了,但必须借助图形.
(1)当P在线段AB上时,由PA=2PB及AB=60cm,可求得PA=40cm,OP=60cm,故点P运动时间为20秒.
点Q运动到的位置恰好是线段AP的中点BQ=40cm,CQ=50cm,点Q的运动速度为
50÷20=![]() (cm/s);
(cm/s);
(2)设运动时间为t秒,则3t+5t=90±70,t=![]() 秒或20秒,
秒或20秒,
∵点Q运动到O点时停止运动,
∴点Q最多运动18秒,当点Q运动18秒到点O时PQ=OP=54cm,之后点P继续运动![]() 秒,
秒,
则PQ=OP=70cm,此时t=![]() 秒,
秒,
∴经过![]() 秒或
秒或![]() 秒两点相距70cm;
秒两点相距70cm;
(3)如图1,设设运动时间为t秒,OP=3t,点P在线段AB上,
![]()
OC﹣OP=90﹣3t
EF=OF﹣OE=45-1.5t
∴ ![]()
另法∵OE=![]() ,OF=
,OF=![]()
∴EF=OF-OE=![]() -
-![]() =
=![]() (OC-OP)
(OC-OP)
∴![]() =2
=2


科目:初中数学 来源: 题型:
【题目】暑假期间,学校组织学生去某景点游玩,甲旅行社说:“如果带队的一名老师购买全票,则学生享受半价优惠”; 乙旅行社说:“所有人按全票价的六折优惠”.已知全票价为a元,学生有x人,带队老师有1人.
(1)试用含a和x的式子表示甲、乙旅行社的收费;
(2)若有30名学生参加本次活动,请你为他们选择一家更优惠的旅行社.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为组织代表队参加市“拜炎帝、诵经典”吟诵大赛,初赛后对选手成绩进行了整理,分成5个小组(x表示成绩,单位:分),A组:75≤x<80;B组:80≤x<85;C组:85≤x<90;D组:90≤x<95;E组:95≤x<100.并绘制出如图两幅不完整的统计图.

请根据图中信息,解答下列问题:
(1)参加初赛的选手共有 名,请补全频数分布直方图;
(2)扇形统计图中,C组对应的圆心角是多少度?E组人数占参赛选手的百分比是多少?
(3)学校准备组成8人的代表队参加市级决赛,E组6名选手直接进入代表队,现要从D组中的两名男生和两名女生中,随机选取两名选手进入代表队,请用列表或画树状图的方法,求恰好选中一名男生和一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB=CD,对角线AC,BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,连接AF,CE,若DE=BF,则下列结论:①CF=AE;②OE=OF;③四边形ABCD是平行四边形;④图中共有四对全等三角形.其中正确结论的个数是
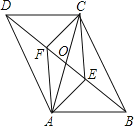
A.4 B.3 C.2 D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学问题:用边长相等的正三角形、正方形和正六边形能否进行平面图形的镶嵌?
问题探究:为了解决上述数学问题,我们采用分类讨论的思想方法去进行探究.
探究一:从正三角形、正方形和正六边形中任选一种图形,能否进行平面图形的镶嵌?
第一类:选正三角形.因为正三角形的每一个内角是60°,所以在镶嵌平面时,围绕某一点有6个正三角形的内角可以拼成一个周角,所以用正三角形可以进行平面图形的镶嵌.
第二类:选正方形.因为正方形的每一个内角是90°,所以在镶嵌平面时,围绕某一点有4个正方形的内角可以拼成一个周角,所以用正方形也可以进行平面图形的镶嵌.
第三类:选正六边形.(仿照上述方法,写出探究过程及结论)
探究二:从正三角形、正方形和正六边形中任选两种图形,能否进行平面图形的镶嵌?
第四类:选正三角形和正方形
在镶嵌平面时,设围绕某一点有x个正三角形和y个正方形的内角可以拼成个周角.根据题意,可得方程
60x+90y=360
整理,得2x+3y=12.
我们可以找到唯一组适合方程的正整数解为![]() .
.
镶嵌平面时,在一个顶点周围围绕着3个正三角形和2个正方形的内角可以拼成一个周角,所以用正三角形和正方形可以进行平面镶嵌
第五类:选正三角形和正六边形.(仿照上述方法,写出探究过程及结论)
第六类:选正方形和正六边形,(不写探究过程,只写出结论)
探究三:用正三角形、正方形和正六边形三种图形是否可以镶嵌平面?
第七类:选正三角形、正方形和正六边形三种图形.(不写探究过程,只写结论),
查看答案和解析>>
科目:初中数学 来源: 题型:
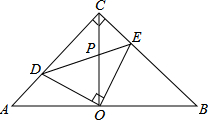
【题目】如图,在等腰直角△ABC中,∠ACB=90°,O是斜边AB的中点,点D,E分别在直角边AC,BC上,且∠DOE=90°,DE交OC于点P.则下列结论:(1)AD+BE=AC;(2)AD2+BE2=DE2;(3)△ABC的面积等于四边形CDOE面积的2倍;(4)OD=OE.其中正确的结论有( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,A、B为x轴上两点,C、D为y轴上的两点,经过点A、C、B的抛物线的一部分c1与经过点A、D、B的抛物线的一部分c2组合成一条封闭曲线,我们把这条封闭曲线成为“蛋线”.已知点C的坐标为(0,﹣![]() ),点M是抛物线C2:y=mx2﹣2mx﹣3m(m<0)的顶点.
),点M是抛物线C2:y=mx2﹣2mx﹣3m(m<0)的顶点.
(1)求A、B两点的坐标;
(2)“蛋线”在第四象限上是否存在一点P,使得△PBC的面积最大?若存在,求出△PBC面积的最大值;若不存在,请说明理由;
(3)当△BDM为直角三角形时,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
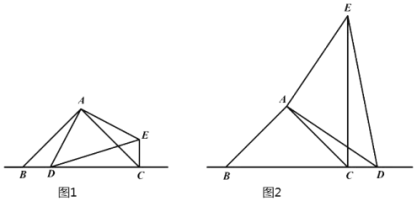
【题目】已知:△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点D是等腰直角三角形ABC斜边BC所在直线上一点(不与点B重合).
(1)如图1,当点D在线段BC上时,线段CE、BD之间的位置关系是__________,数量关系是___________;
(2)如图2,当点D在线段BC的延长线上时,探索AD、BD、CD三条线段之间的数量关系,写出结论并证明;
(3)若BD=![]() CD,直接写出∠BAD的度数。
CD,直接写出∠BAD的度数。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com