
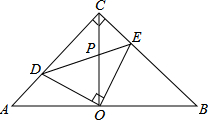
【题目】如图,在等腰直角△ABC中,∠ACB=90°,O是斜边AB的中点,点D,E分别在直角边AC,BC上,且∠DOE=90°,DE交OC于点P.则下列结论:(1)AD+BE=AC;(2)AD2+BE2=DE2;(3)△ABC的面积等于四边形CDOE面积的2倍;(4)OD=OE.其中正确的结论有( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
由等腰直角三角形的性质可得AC=BC,CO=AO=BO,∠ACO=∠BCO=∠A=∠B=45°,CO⊥AO,由“ASA”可证△ADO≌△CEO,△CDO≌△BEO,由全等三角形的性质可依次判断.
∵在等腰直角△ABC中,∠ACB=90°,O是斜边AB的中点,
∴AC=BC,CO=AO=BO,∠ACO=∠BCO=∠A=∠B=45°,CO⊥AO
∵∠DOE=90°,
∴∠COD+∠COE=90°,且∠AOD+∠COD=90°
∴∠COE=∠AOD,且AO=CO,∠A=∠ACO=45°,
∴△ADO≌△CEO(ASA)
∴AD=CE,OD=OE,故④正确,
同理可得:△CDO≌△BEO
∴CD=BE,
∴AC=AD+CD=AD+BE,故①正确,
在Rt△CDE中,CD2+CE2=DE2,
∴AD2+BE2=DE2,故②正确,
∵△ADO≌△CEO,△CDO≌△BEO
∴S△ADO=S△CEO,S△CDO=S△BEO,
∴△ABC的面积等于四边形CDOE面积的2倍;故③正确,
综上所述:正确的结论有①②③④,
故选D.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:
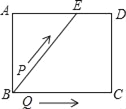
【题目】如图,矩形ABCD中,AB=4cm,AD=5cm,点E在AD上,且AE=3cm,点P、Q同时从点B出发,点P沿BE→ED→DC运动到点C停止,点Q沿BC运动到点C停止,它们的运动速度都是1cm/s,设P、Q出发t秒,△BPQ的面积为y cm2.则y与t的函数关系图象大致是( )
A. 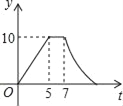 B.
B.  C.
C. 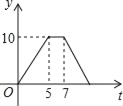 D.
D. 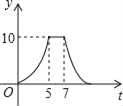
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八(1)班组织了一次经典诵读比赛,甲、乙两队各10人的比赛成绩如下表:
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的方差;
(3)已知甲队成绩的方差是1.4,则成绩较为整齐的是 队.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的角平分线,以AD为弦的⊙O交AB、AC于E、F,已知EF∥BC.
(1)求证:BC是⊙O的切线;
(2)若已知AE=9,CF=4,求DE长;
(3)在(2)的条件下,若∠BAC=60°,求tan∠AFE的值及GD长.
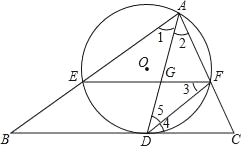
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中的位置如图所示.
(1)将△ABC向下平移3个单位长度,再向右平移2个单位长度,画出平移后的△A1B1C1;并写出顶点A1、B1、C1各点的坐标;
(2)计算△A1B1C1的面积。
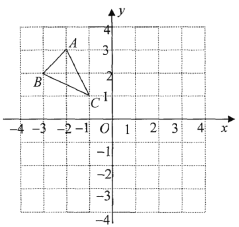
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AD=2AB,E是BC的中点,连结AE并延长交DC的延长线于点F.
(1)求证:DE⊥AF;
(2)若∠B=60°,DE=4,求AB的长,
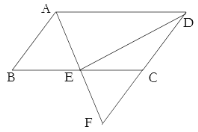
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:在![]() 中,
中,![]() ,
,![]() .
.
(1)按下列步骤用尺规作图(保留作图痕迹,不写出作法):作![]() 的平分线AD,交BC于D;
的平分线AD,交BC于D;
(2)在(1)中,过点D作![]() ,交AB于点E,若CD=4,则BC的长为 .
,交AB于点E,若CD=4,则BC的长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某课题小组为了了解某品牌电动自行车的销售情况,对某专卖店第一季度该品牌A、B、C、D四种型号的销售做了统计,绘制成如下两幅统计图(均不完整)
(1)该店第一季度售出这种品牌的电动自行车共多少辆?
(2)把两幅统计图补充完整;
(3)若该专卖店计划订购这四款型号的电动自行车1800辆,求C型电动自行车应订购多少辆?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个运输公司有甲、乙两种货车,两次满载的运输情况如下表:
甲种货车辆数 | 乙种货车辆数 | 合计运货吨数 | |
第一次 | 2 | 4 | 18 |
第二次 | 5 | 6 | 35 |
(1)求甲、乙两种货车每次满载分别能运输多少吨货物;
(2)现有一批重34吨的货物需要运输,而甲、乙两种货车运输的保养费用分别为80元/辆和40元/辆.公司打算由甲、乙两种货车共10辆来完成这次运输,为了使保养费用不超过700元,公司该如何安排甲、乙两种货车来完成这次运输任务.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com