
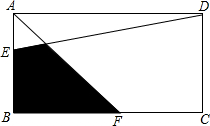
 面积为1的长方形ABCD中,点E为AB的三等分点,点F为BC中点,求阴影部分的面积.
面积为1的长方形ABCD中,点E为AB的三等分点,点F为BC中点,求阴影部分的面积. 分析 延长AF,DC交于P点,CP=DC=1,再根据相似三角形的判定和性质解答即可.
解答 解:延长AF,DC交于P点,CP=DC=1,如图: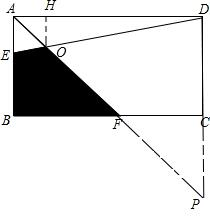
∴PF=AF,
∴△AEC∽△DOP,
∴$\frac{EO}{OD}=\frac{AE}{DP}=\frac{\frac{1}{3}}{2}=\frac{1}{6}$,
过O作OH⊥AD,
$\frac{OH}{AE}=\frac{DO}{DE}=\frac{6}{7}$,
$OH=AE×\frac{6}{7}=\frac{2}{7}$,
∴${S}_{△AOD}=\frac{1}{2}OH•AD=\frac{1}{7}$,
${S}_{阴影}={S}_{正方形}-{S}_{△AED}-{S}_{梯形ADCF}+{S}_{△AOD}=1-\frac{1}{6}-\frac{3}{4}+\frac{1}{7}=\frac{19}{84}$.
点评 此题考查矩形的性质,关键是根据矩形的性质和相似三角形的判定和性质分析.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 质量m(千克) | 0 | 1 | 2 | 3 | 4 | 5 | … |
| 售价s(元) | 2 | 2.3 | 2.6 | 2.9 | 3.2 | 3.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com