
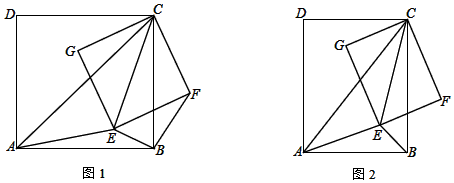
分析 (1)①首先根据四边形ABCD和EFCG均为正方形,可得$\frac{AC}{BC}$=$\frac{CE}{CF}$=$\sqrt{2}$,∠ACE=∠BCF;然后根据相似三角形判定的方法,推得△CAE∽△CBF即可;
②首先根据△CAE∽△CBF,判断出∠CAE=∠CBF,再根据∠CAE+∠CBE=90°,判断出∠EBF=90°;然后在Rt△BEF中,根据勾股定理,求出EF的长度,再根据CE、EF的关系,求出CE的长是多少即可.
(2)首先根据相似三角形判定的方法,判断出△ACE∽△BCF,即可判断出$\frac{AE}{BF}$=$\frac{AC}{BC}$=$\sqrt{{k}^{2}+1}$,据此求出BF的长度是多少;然后判断出∠EBF=90°,在Rt△BEF中,根据勾股定理,求出EF的值是多少,进而求出k的值是多少即可.
解答 (1)证明:
①∵四边形ABCD和EFCG均为正方形,
∴$\frac{AC}{BC}$=$\frac{CE}{CF}$=$\sqrt{2}$,
∵∠ACB=∠ECF=45°,
∴∠ACE=∠BCF,
∴△CAE∽△CBF;
②∵△CAE∽△CBF,
∴∠CBF=∠CAE,$\frac{AE}{BF}$=$\sqrt{2}$,
∵AE=2,
∴BF=$\sqrt{2}$,
∵∠CAE+∠CBE=90°,
∴∠CBF+∠CBE=90°,
在Rt△EBF中,EF=$\sqrt{B{E}^{2}+B{F}^{2}}$=$\sqrt{3}$,
∵四边形EFCG为正方形,
∴CE=$\sqrt{2}$EF=$\sqrt{6}$;
(3)连接BF,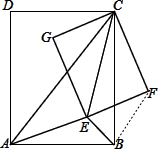
∵$\frac{AB}{BC}$=$\frac{EF}{FC}$,∠ABC=∠EFC=90°,
∴Rt△ABC∽Rt△CEF,
∴$\frac{CA}{CB}$=$\frac{CE}{CF}$,
又∠ACB=∠ECF,
∴∠ACE=∠BCF,
∴△ACE∽△BCF,
∴$\frac{AE}{BF}$=$\frac{AC}{BC}$=$\sqrt{{k}^{2}+1}$,
∵AE=2,
∴BF=$\frac{2}{\sqrt{{k}^{2}+1}}$,
∵∠EBF=90°,
∴EF2=BE2+BF2=1+$\frac{4}{{k}^{2}+1}$,
∵CE=$\sqrt{1+\frac{1}{{k}^{2}}}$EF,
∴CE2=(1+$\frac{1}{{k}^{2}}$)(1+$\frac{4}{{k}^{2}+1}$)=9,解得k=$\frac{\sqrt{10}}{4}$或k=-$\frac{\sqrt{10}}{4}$(不合题意,舍去),
故答案为:$\frac{\sqrt{10}}{4}$.
点评 本题为四边形的综合应用,涉及正方形、矩形的性质、相似三角形的判定和性质、勾股定理、方程思想等知识.在(1)中利用正方形的性质找到三角形相似的条件是解题的关键,在(2)中连接BF,把问题转化成(1)的形式是解题的关键.本题考查知识点较多,综合性较强,难度较大.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:在一条东西向的双轨铁路上迎面驶来一快一慢两列火车,快车长AB=2(单位长度).慢车长CD=4(单位长度),设正在行驶途中的某一时刻,如图,以两车之间的某点O为原点,取向右方向为正方向画数轴,此时快车A在数轴上表示的数是a,慢车头C在数轴上表示的数是b,若快车AB以6个单位长度/秒的速度向右匀速继续行驶,同时慢车CD以4个单位长度/秒的速度向左匀速继续行驶,且|a+6|与(b-18)2互为相反数.
已知:在一条东西向的双轨铁路上迎面驶来一快一慢两列火车,快车长AB=2(单位长度).慢车长CD=4(单位长度),设正在行驶途中的某一时刻,如图,以两车之间的某点O为原点,取向右方向为正方向画数轴,此时快车A在数轴上表示的数是a,慢车头C在数轴上表示的数是b,若快车AB以6个单位长度/秒的速度向右匀速继续行驶,同时慢车CD以4个单位长度/秒的速度向左匀速继续行驶,且|a+6|与(b-18)2互为相反数.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com