
【题目】设k是任意实数,讨论关于x的方程|x2﹣1|=x+k的解的个数.
【答案】答案见解析.
【解析】
先根据x的范围去绝对值,(1)当x>1或x<﹣1,方程变为x2﹣x=1+k,要求方程解的个数就是要二次函数y=x2﹣x与直线y=1+k的交点个数,可求出二次函数y=x2﹣x的顶点(![]() ,-
,-![]() ),且过(0,0),(1,0)两点,则当1+k<0,原方程无实根;当1+k≥2,原方程有两个实根;当0≤1+k<2,原方程有一个实根;当1+k<0,原方程无实根.(2)当﹣1≤x≤1,方程变为x2+x=1﹣k,和(1)的解法一样求出k的范围.
),且过(0,0),(1,0)两点,则当1+k<0,原方程无实根;当1+k≥2,原方程有两个实根;当0≤1+k<2,原方程有一个实根;当1+k<0,原方程无实根.(2)当﹣1≤x≤1,方程变为x2+x=1﹣k,和(1)的解法一样求出k的范围.
解:(1)当x>1或x<﹣1,方程变为x2﹣x=1+k,则方程解的个数就是二次函数y=x2﹣x与直线y=1+k的交点个数,二次函数y=x2﹣x的顶点(![]() ,-
,-![]() ),且过(0,0),(1,0)两点.
),且过(0,0),(1,0)两点.
当0≤1+k<2,即﹣1≤k<1,二次函数y=x2﹣x与直线y=1+k在所在范围有一个交点,所以原方程有一个实根;
当1+k≥2,即k≥1,二次函数y=x2﹣x与直线y=1+k在所在范围有两个交点,所以原方程有两个实根;
当1+k<0,即k<﹣1,二次函数y=x2﹣x与直线y=1+k无交点,所以原方程无实根.
(2)当﹣1≤x≤1,方程变为x2+x=1﹣k,则方程解的个数就是二次函数y=x2+x与直线y=1﹣k的交点个数,二次函数y=x2+x的顶点(-![]() ,-
,-![]() ),且过(0,0),(﹣1,0)两点.
),且过(0,0),(﹣1,0)两点.
当1﹣k>0,即k<1,二次函数y=x2+x与直线y=1﹣k在所在范围无交点,所以原方程无实根;
当-![]() <1﹣k≤0,即1≤k<
<1﹣k≤0,即1≤k<![]() ,二次函数y=x2+x与直线y=1﹣k有两个交点,所以原方程有两个实根;
,二次函数y=x2+x与直线y=1﹣k有两个交点,所以原方程有两个实根;
当1﹣k=-![]() ,即k=
,即k=![]() ,二次函数y=x2+x与直线y=1﹣k有一个交点,所以原方程有一个实根;
,二次函数y=x2+x与直线y=1﹣k有一个交点,所以原方程有一个实根;
当1﹣k<-![]() ,即k>
,即k>![]() ,二次函数y=x2+x与直线y=1﹣k没有交点,所以原方程无实根.
,二次函数y=x2+x与直线y=1﹣k没有交点,所以原方程无实根.
所以当k<﹣![]() 或﹣1<k<1或k>
或﹣1<k<1或k>![]() 时,原方程没有实数根;当k=﹣
时,原方程没有实数根;当k=﹣![]() 或k=
或k=![]() 时,原方程只有一个实数根;当-
时,原方程只有一个实数根;当-![]() <k≤﹣1或1≤k<
<k≤﹣1或1≤k<![]() 时,原方程有两个实数根.
时,原方程有两个实数根.


科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,BO、CO是角平分线.
(1)∠ABC=50°,∠ACB=60°,求∠BOC的度数,并说明理由.
(2)题(1)中,如将“∠ABC=50°,∠ACB=60°”改为“∠A=70°”,求∠BOC的度数.
(3)若∠A=n°,求∠BOC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将矩形OABC置于平面直角坐标系中,点A的坐标为(0,4),点C的坐标为(m,0)(m>0),点D(m,1)在BC上,将矩形OABC沿AD折叠压平,使点B的对应点E落在坐标平面内,当△ADE是等腰直角三角形时,点E的坐标为______.
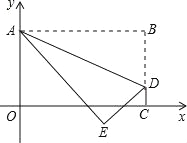
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A(1,a)是反比例函数y=﹣![]() 的图象上一点,直线y=﹣
的图象上一点,直线y=﹣![]() x+
x+![]() 与反比例函数y=﹣
与反比例函数y=﹣![]() 的图象在第四象限的交点为点B,动点P(x,0)在x轴的正半轴上运动,当线段PA与线段PB之差达到最大时,则点P的坐标是_____.
的图象在第四象限的交点为点B,动点P(x,0)在x轴的正半轴上运动,当线段PA与线段PB之差达到最大时,则点P的坐标是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,A(﹣3,0)、B(0,7)、C(7,0),∠ABC+∠ADC=180°,BC⊥CD.
(1)求证:∠ABO=∠CAD;
(2)求四边形ABCD的面积;
(3)如图2,E为∠BCO的邻补角的平分线上的一点,且∠BEO=45°,OE交BC于点F,求BF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2﹣4与x轴交于点A,B(点A位于点B的左侧),C为顶点,直线y=x+m经过点A,与y轴交于点D.
(1)求线段AD的长;
(2)平移该抛物线得到一条新拋物线,设新抛物线的顶点为C′.若新抛物线经过点D,并且新抛物线的顶点和原抛物线的顶点的连线CC′平行于直线AD,求新抛物线对应的函数表达式.
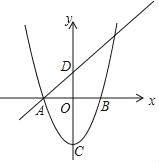
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2015南通)如图,在ABCD中,点E,F分别在AB,DC上,且ED⊥DB,FB⊥BD.
(1)求证:△AED≌△CFB;
(2)若∠A=30°,∠DEB=45°,求证:DA=DF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线![]()
![]() 与双曲线
与双曲线![]() 的一个交点为P(2,m),与x轴、y轴分别交于点A,B.
的一个交点为P(2,m),与x轴、y轴分别交于点A,B.
(1)求m的值;
(2)若PA=2AB,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某电信公司提供了A,B两种方案的移动通讯费用y(元)与通话时间x(元)之间的关系,则下列结论中正确的有( )
(1)若通话时间少于120分,则A方案比B方案便宜20元;
(2)若通话时间超过200分,则B方案比A方案便宜12元;
(3)若通讯费用为60元,则B方案比A方案的通话时间多;
(4)若两种方案通讯费用相差10元,则通话时间是145分或185分.

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com