
【题目】如图1,在平面直角坐标系中,A(﹣3,0)、B(0,7)、C(7,0),∠ABC+∠ADC=180°,BC⊥CD.
(1)求证:∠ABO=∠CAD;
(2)求四边形ABCD的面积;
(3)如图2,E为∠BCO的邻补角的平分线上的一点,且∠BEO=45°,OE交BC于点F,求BF的长.

【答案】(1)见解析;(2)50;(3)7.
【解析】
(1)根据四边形的内角和定理、直角三角形的性质证明;
(2)过点A作AF⊥BC于点F,作AE⊥CD的延长线于点E,作DG⊥x轴于点G,证明△ABF≌△ADE、△ABO≌△DAG,得到D点的坐标为(4,﹣3),根据三角形的面积公式计算;
(3)作EH⊥BC于点H,作EG⊥x轴于点G,根据角平分线的性质得到EH=EG,证明△EBH≌△EOG,得到EB=EO,根据等腰三角形的判定定理解答.
(1)在四边形ABCD中,
∵∠ABC+∠ADC=180°,
∴∠BAD+∠BCD=180°,
∵BC⊥CD,
∴∠BCD=90°,
∴∠BAD=90°,
∴∠BAC+∠CAD=90°,
∵∠BAC+∠ABO=90°,
∴∠ABO=∠CAD;
(2)过点A作AF⊥BC于点F,作AE⊥CD的延长线于点E,作DG⊥x轴于点G,如图1
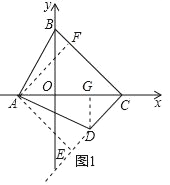
∵B(0,7),C(7,0),
∴OB=OC,
∴∠BCO=45°,
∵BC⊥CD,
∴∠BCO=∠DCO=45°,
∵AF⊥BC,AE⊥CD,
∴AF=AE,∠FAE=90°,
∴∠BAF=∠DAE,
在△ABF和△ADE中,
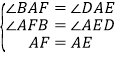 ,
,
∴△ABF≌△ADE(AAS),
∴AB=AD,
同理,△ABO≌△DAG,
∴DG=AO,BO=AG,
∵A(﹣3,0)B(0,7),
∴D(4,﹣3),
S四ABCD=![]() AC(BO+DG )=50;
AC(BO+DG )=50;
(3)过点E作EH⊥BC于点H,作EG⊥x轴于点G,如图2
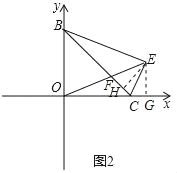
∵E点在∠BCO的邻补角的平分线上,
∴EH=EG,
∵∠BCO=∠BEO=45°,
∴∠EBC=∠EOC,
在△EBH和△EOG中,
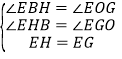 ,
,
∴△EBH≌△EOG(AAS),
∴EB=EO,
∵∠BEO=45°,
∴∠EBO=∠EOB=67.5°,又∠OBC=45°,
∴∠BOE=∠BFO=67.5°,
∴BF=BO=7.


科目:初中数学 来源: 题型:
【题目】某市的连锁超市总部为了解各超市的销售情况,统计了各超市在某月的销售额(单位:万元),并根据统计的这组销售额数据,绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
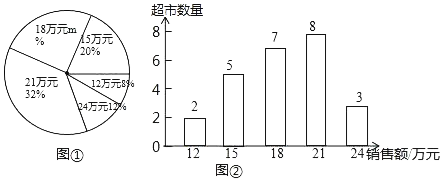
(I)该市的连锁超市总数为 ,图①中m的值为 ;
(II)求统计的这组销售额数据的平均数、众数和中位数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列图形,它是把一个三角形分别连接这个三角形三边的中点,构成4个小三角形,挖去中间的一个小三角形(如图1);对剩下的三个小三角形再分别重复以上做法,…将这种做法继续下去(如图2,图3…),则图6中挖去三角形的个数为( ) 
A.121
B.362
C.364
D.729
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠1=∠2,则不一定能使△ABD≌△ACD的条件是 ( )

A. AB=AC B. BD=CD C. ∠B=∠C D. ∠BDA=∠CDA
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2015攀枝花)某超市销售有甲、乙两种商品,甲商品每件进价10元,售价15元;乙商品每件进价30元,售价40元.
(1)若该超市一次性购进两种商品共80件,且恰好用去1600元,问购进甲、乙两种商品各多少件?
(2)若该超市要使两种商品共80件的购进费用不超过1640元,且总利润(利润=售价﹣进价)不少于600元.请你帮助该超市设计相应的进货方案,并指出使该超市利润最大的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图BE//CF,BE、CF分别平分∠ABC和∠BCD, 求证:AB//CD

证明:∵ BE、CF分别平分∠ABC和∠BCD(已知)
∴ ∠1=![]() ∠ ∠2=
∠ ∠2=![]() ∠ ( )
∠ ( )
∵ BE//CF( )
∴ ∠1=∠2( )
∴ ![]() ∠ABC=
∠ABC=![]() ∠BCD
∠BCD
即∠ABC=∠BCD
∴ AB//CD( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,且AD=12cm.点P从点A出发,以3cm/s的速度在射线AD上运动;同时,点Q从点C出发,以1cm/s的速度在射线CB上运动.运动时间为t,当t=______秒(s)时,点P、Q、C、D构成平行四边形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com