
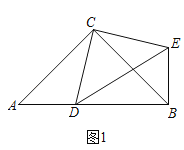
ЁОЬтФПЁПЃЈ1ЃЉЮЪЬтЗЂЯж
ШчЭМ1ЃЌдкRtЁїABCКЭRtЁїCDEжаЃЌЁЯACBЃНЁЯDCEЃН90ЁуЃЌЁЯCABЃНЁЯCDEЃН45ЁуЃЌЕуDЪБЯпЖЮABЩЯвЛЖЏЕуЃЌСЌНгBEЃЎ
ЬюПеЃКЂй![]() ЕФжЕЮЊЁЁ ЁЁЃЛ ЂкЁЯDBEЕФЖШЪ§ЮЊЁЁ ЁЁЃЎ
ЕФжЕЮЊЁЁ ЁЁЃЛ ЂкЁЯDBEЕФЖШЪ§ЮЊЁЁ ЁЁЃЎ
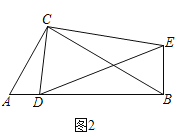
ЃЈ2ЃЉРрБШЬНОП
ШчЭМ2ЃЌдкRtЁїABCКЭRtЁїCDEжаЃЌЁЯACBЃНЁЯDCEЃН90ЁуЃЌЁЯCABЃНЁЯCDEЃН60ЁуЃЌЕуDЪЧЯпЖЮABЩЯвЛЖЏЕуЃЌСЌНгBEЃЎЧыХаЖЯ![]() ЕФжЕМАЁЯDBEЕФЖШЪ§ЃЌВЂЫЕУїРэгЩЃЛ
ЕФжЕМАЁЯDBEЕФЖШЪ§ЃЌВЂЫЕУїРэгЩЃЛ
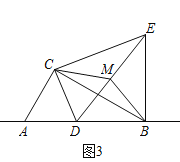
ЃЈ3ЃЉЭиеЙбгЩь
ШчЭМ3ЃЌдкЃЈ2ЃЉЕФЬѕМўЯТЃЌНЋЕуDИФЮЊжБЯпABЩЯвЛЖЏЕуЃЌЦфгрЬѕМўВЛБфЃЌШЁЯпЖЮDEЕФжаЕуMЃЌСЌНгBMЁЂCMЃЌШєACЃН2ЃЌдђЕБЁїCBMЪЧжБНЧШ§НЧаЮЪБЃЌЯпЖЮBEЕФГЄЪЧЖрЩйЃПЧыжБНгаДГіД№АИЃЎ
ЁОД№АИЁПЃЈ1ЃЉЂй1ЃЛ Ђк90ЁуЃЛЃЈ2ЃЉ![]() ЃН
ЃН![]() ЃЌЁЯDBEЃН90ЁуЃЌРэгЩМћНтЮіЃЛЃЈ3ЃЉBEЕФГЄЮЊ3+
ЃЌЁЯDBEЃН90ЁуЃЌРэгЩМћНтЮіЃЛЃЈ3ЃЉBEЕФГЄЮЊ3+![]() Лђ3Љ
Лђ3Љ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉгЩжБНЧШ§НЧаЮЕФаджЪПЩЕУЁЯABCЃН45ЁуЃЌПЩЕУЁЯDBEЃН90ЁуЃЌЭЈЙ§жЄУїЁїACDЁзЁїBCEЃЌПЩЕУ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉЭЈЙ§жЄУїЁїACDЁзЁїBCEЃЌПЩЕУ![]() ЕФжЕЃЌЁЯCBEЃНЁЯCADЃН60ЁуЃЌМДПЩЧѓЁЯDBEЕФЖШЪ§ЃЛ
ЕФжЕЃЌЁЯCBEЃНЁЯCADЃН60ЁуЃЌМДПЩЧѓЁЯDBEЕФЖШЪ§ЃЛ
ЃЈ3ЃЉЗжЕуDдкЯпЖЮABЩЯКЭBAбгГЄЯпЩЯСНжжЧщПіЬжТлЃЌгЩжБНЧШ§НЧаЮЕФаджЪПЩжЄCMЃНBMЃН![]() ЃЌМДПЩЧѓDEЃН2
ЃЌМДПЩЧѓDEЃН2![]() ЃЌгЩЯрЫЦШ§НЧаЮЕФаджЪПЩЕУЁЯABEЃН90ЁуЃЌBEЃН
ЃЌгЩЯрЫЦШ§НЧаЮЕФаджЪПЩЕУЁЯABEЃН90ЁуЃЌBEЃН![]() ADЃЌгЩЙДЙЩЖЈРэПЩЧѓBEЕФГЄЃЎ
ADЃЌгЩЙДЙЩЖЈРэПЩЧѓBEЕФГЄЃЎ
НтЃКЃЈ1ЃЉЁпЁЯACBЃН90ЁуЃЌЁЯCABЃН45ЁуЃЌ
ЁрЁЯABCЃНЁЯCABЃН45ЁуЃЌ
ЁрACЃНBCЃЌЁЯDBEЃНЁЯABC+ЁЯCBEЃН90ЁуЃЌ
ЁпЁЯACBЃНЁЯDCEЃН90ЁуЃЌ
ЁрЁЯACDЃНЁЯBCEЃЌЧвЁЯCABЃНЁЯCDEЃН45ЁуЃЌ
ЁрЁїACDЁзЁїBCEЃЌ
Ёр![]() ЃЌ
ЃЌ
ЙЪД№АИЮЊЃК1ЃЌ90ЁуЃЛ
ЃЈ2ЃЉ![]() ЃЌЁЯDBEЃН90ЁуЃЛ
ЃЌЁЯDBEЃН90ЁуЃЛ
РэгЩЃКЁпЁЯACBЃНЁЯDCEЃН90ЁуЃЌЁЯCABЃНЁЯCDEЃН60ЁуЃЌ
ЁрЁЯACDЃНЁЯBCEЃЌЁЯCEDЃНЁЯABCЃН30ЁуЃЌ
ЁрtanЁЯABCЃНtan30ЁуЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁпЁЯACBЃНЁЯDCEЃН90ЁуЃЌЁЯCABЃНЁЯCDEЃН60ЁуЃЌ
ЁрRtЁїACBЁзRtЁїDCEЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌЧвЁЯACDЃНЁЯBCEЃЌ
ЃЌЧвЁЯACDЃНЁЯBCEЃЌ
ЁрЁїACDЁзЁїBCEЃЌ
Ёр![]() ЃН
ЃН![]() ЃЌЁЯCBEЃНЁЯCADЃН60ЁуЃЌ
ЃЌЁЯCBEЃНЁЯCADЃН60ЁуЃЌ
ЁрЁЯDBEЃНЁЯABC+ЁЯCBEЃН90ЁуЃЛ
ЃЈ3ЃЉШєЕуDдкЯпЖЮABЩЯЃЌШчЭМЃЌ
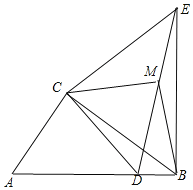
гЩЃЈ2ЃЉжЊЃК![]() ЃН
ЃН![]() ЃЌЁЯABEЃН90ЁуЃЌ
ЃЌЁЯABEЃН90ЁуЃЌ
ЁрBEЃН![]() ADЃЌ
ADЃЌ
ЁпACЃН2ЃЌЁЯACBЃН90ЁуЃЌЁЯCABЃН90ЁуЃЌ
ЁрABЃН4ЃЌBCЃН2![]() ЃЌ
ЃЌ
ЁпЁЯECDЃНЁЯABEЃН90ЁуЃЌЧвЕуMЪЧDEжаЕуЃЌ
ЁрCMЃНBMЃН![]() DEЃЌ
DEЃЌ
ЧвЁїCBMЪЧжБНЧШ§НЧаЮЃЌ
ЁрCM2+BM2ЃНBC2ЃНЃЈ2![]() ЃЉ2ЃЌ
ЃЉ2ЃЌ
ЁрBMЃНCMЃН![]() ЃЌ
ЃЌ
ЁрDEЃН2![]() ЃЌ
ЃЌ
ЁпDB2+BE2ЃНDE2ЃЌ
ЁрЃЈ4ЉADЃЉ2+ЃЈ![]() ADЃЉ2ЃН24ЃЌ
ADЃЉ2ЃН24ЃЌ
ЁрADЃН![]() +1ЃЌ
+1ЃЌ
ЁрBEЃН![]() ADЃН3+
ADЃН3+![]() ЃЛ
ЃЛ
ШєЕуDдкЯпЖЮBAбгГЄЯпЩЯЃЌШчЭМЃЌ
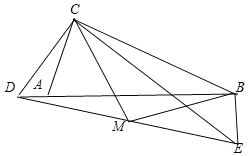
ЭЌРэПЩЕУЃКDEЃН2![]() ЃЌBEЃН
ЃЌBEЃН![]() ADЃЌ
ADЃЌ
ЁпBD2+BE2ЃНDE2ЃЌ
ЁрЃЈ4+ADЃЉ2+ЃЈ![]() ADЃЉ2ЃН24ЃЌ
ADЃЉ2ЃН24ЃЌ
ЁрADЃН![]() Љ1ЃЌ
Љ1ЃЌ
ЁрBEЃН![]() ADЃН3Љ
ADЃН3Љ![]() ЃЌ
ЃЌ
злЩЯЫљЪіЃКBEЕФГЄЮЊ3+![]() Лђ3Љ
Лђ3Љ![]() .
.


 гЎдкПЮЬУУћЪІПЮЪБМЦЛЎЯЕСаД№АИ
гЎдкПЮЬУУћЪІПЮЪБМЦЛЎЯЕСаД№АИ ЬьЬьЯђЩЯПЮЪБЭЌВНбЕСЗЯЕСаД№АИ
ЬьЬьЯђЩЯПЮЪБЭЌВНбЕСЗЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§![]() ЕФЖЅЕузјБъЮЊ
ЕФЖЅЕузјБъЮЊ![]() ЃЌ
ЃЌ![]() .
.
ЃЈ1ЃЉШєИУКЏЪ§ЭМЯѓЙ§Еу![]() .
.
ЂйЧѓИУКЏЪ§НтЮіЪНЃЛ
Ђк![]() ЃЌКЏЪ§ЭМЯѓЩЯЕу
ЃЌКЏЪ§ЭМЯѓЩЯЕу![]() ЕНxжсЕФОрРызюаЁжЕЮЊ1ЃЌдђtЕФжЕЮЊ______ЃЛ
ЕНxжсЕФОрРызюаЁжЕЮЊ1ЃЌдђtЕФжЕЮЊ______ЃЛ
ЃЈ2ЃЉШєЕуPдкКЏЪ§![]() ЕФЭМЯѓЩЯЃЌЧв
ЕФЭМЯѓЩЯЃЌЧв![]() ЃЌЧѓhЕФзюДѓжЕ.
ЃЌЧѓhЕФзюДѓжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
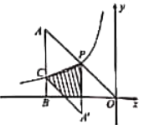
ЁОЬтФПЁПШчЭМЕуPЮЊЫЋЧњЯп![]() ЩЯвЛЖЏЕу.СЌНгOPВЂбгГЄЕНЕуAЃЌЪЙ
ЩЯвЛЖЏЕу.СЌНгOPВЂбгГЄЕНЕуAЃЌЪЙ![]() ЃЌЙ§ЕуAзїxжсЕФДЙЯпЃЌДЙзуЮЊBЃЌНЛЫЋЧњЯпгкЕуC.ЕБ
ЃЌЙ§ЕуAзїxжсЕФДЙЯпЃЌДЙзуЮЊBЃЌНЛЫЋЧњЯпгкЕуC.ЕБ![]() ЪБЃЌСЌНгPCЃЌНЋ
ЪБЃЌСЌНгPCЃЌНЋ![]() бижБЯпPCНјааЗелЃЌдђЗелКѓЕФ
бижБЯпPCНјааЗелЃЌдђЗелКѓЕФ![]() гыЫФБпаЮBOPCЕФжиЕўВПЗжЃЈЭМжавѕгАВПЗжЃЉЕФУцЛ§ЪЧ_______________
гыЫФБпаЮBOPCЕФжиЕўВПЗжЃЈЭМжавѕгАВПЗжЃЉЕФУцЛ§ЪЧ_______________
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
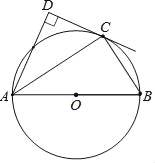
ЁОЬтФПЁПШчЭМЃЌЕуCдквдABЮЊжБОЖЕФЁбOЩЯЃЌADгыЙ§ЕуCЕФЧаЯпДЙжБЃЌДЙзуЮЊЕуDЃЎ
ЃЈ1ЃЉЧѓжЄЃКACЦНЗжЁЯDABЃЛ
ЃЈ2ЃЉЧѓжЄЃКAC2=ADABЃЛ
ЃЈ3ЃЉШєAD=![]() ЃЌsinB=
ЃЌsinB=![]() ЃЌЧѓЯпЖЮBCЕФГЄЃЎ
ЃЌЧѓЯпЖЮBCЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯB=90ЁуЃЌЁЯBACЕФЦНЗжЯпНЛBCгкЕуDЃЌвдDЮЊдВаФЃЌDГЄЮЊАыОЖзїзїЁбD.
ЂХЧѓжЄЃКACЪЧЁбDЕФЧаЯп.
ЂЦЩшACгыЁбDЧагкЕуEЃЌDB=1ЃЌСЌНгDEЃЌBFЃЌEF.
ЂйЕБЁЯBAD= ЪБЃЌЫФБпаЮBDEFЮЊСтаЮЃЛ
ЂкЕБAB= ЪБЃЌЁїCDEЮЊЕШбќШ§НЧаЮ.
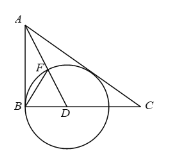
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌPЪЧBCЩЯвЛЖЏЕуЃЌЙ§PзїAPЕФДЙЯпНЛCDгкEЃЌНЋ
ЃЌPЪЧBCЩЯвЛЖЏЕуЃЌЙ§PзїAPЕФДЙЯпНЛCDгкEЃЌНЋ![]() ЗелЕУЕН
ЗелЕУЕН![]() ЃЌбгГЄFPНЛABгкHЃЌСЌНсAEЃЌPEНЛACгкG.
ЃЌбгГЄFPНЛABгкHЃЌСЌНсAEЃЌPEНЛACгкG.

ЃЈ1ЃЉЧѓжЄ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЕБ![]() ЪБЃЌЧѓAEЕФГЄЃЛ
ЪБЃЌЧѓAEЕФГЄЃЛ
ЃЈ3ЃЉЕБ![]() ЪБЃЌЧѓAGЕФГЄ.
ЪБЃЌЧѓAGЕФГЄ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЙигкxЕФвЛдЊЖўДЮЗНГЬЃЈxЉ3ЃЉЃЈxЉ2ЃЉ=|m|ЃЎ
ЃЈ1ЃЉЧѓжЄЃКЖдгкШЮвтЪЕЪ§mЃЌЗНГЬзмгаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЛ
ЃЈ2ЃЉШєЗНГЬЕФвЛИіИљЪЧ1ЃЌЧѓmЕФжЕМАЗНГЬЕФСэвЛИіИљЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкБпГЄЮЊ1ЕФе§ЗНаЮЭјИёжаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ШЦ
ШЦ![]() ЕуЫГЪБеыа§зЊ
ЕуЫГЪБеыа§зЊ![]() ЕУ
ЕУ![]() ЃЈЕу
ЃЈЕу![]() гыЕу
гыЕу![]() ЖдгІЃЉ.
ЖдгІЃЉ.
ЃЈ1ЃЉжБНгаДГі![]() ЕФжЕЃК
ЕФжЕЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉгУЮоПЬЖШжБГпзїГіЕу![]() ВЂжБНгаДГі
ВЂжБНгаДГі![]() ЕФзјБъЃЈБЃСєзїЭМКлМЃЃЌВЛаДзїЗЈЃЉЃЛ
ЕФзјБъЃЈБЃСєзїЭМКлМЃЃЌВЛаДзїЗЈЃЉЃЛ
ЃЈ3ЃЉШєИёЕу![]() дк
дк![]() ЕФНЧЦНЗжЯпЩЯЃЌетбљЕФИёЕу
ЕФНЧЦНЗжЯпЩЯЃЌетбљЕФИёЕу![]() ЃЈВЛАќРЈЕу
ЃЈВЛАќРЈЕу![]() гаЃЉ ИіЃЈжБНгаДГіД№АИЃЉ
гаЃЉ ИіЃЈжБНгаДГіД№АИЃЉ
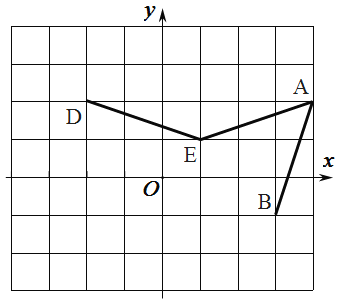
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЕчЯпИЫЩЯЕФCДІв§РЯпCEЁЂCFЙЬЖЈЕчЯпИЫЃЌРЯпCEКЭЕиУцГЩ60ЁуНЧЃЌдкРыЕчЯпИЫ6УзЕФBДІАВжУВтНЧвЧЃЌдкAДІВтЕУЕчЯпИЫЩЯCДІЕФбіНЧЮЊ30ЁуЃЌвбжЊВтНЧвЧИпABЮЊ1.5УзЃЌЧѓРЯпCEЕФГЄЃЈНсЙћБЃСєИљКХЃЉЃЎ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com