
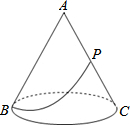
 如图,有一圆锥形粮堆,其正视图是边长为6m的正三角形ABC,粮堆母线AC的中点P处有一老鼠正在偷吃粮食,此时,小猫正在B处,它要沿圆锥侧面到达P处捕捉老鼠,则小猫所经过的最短路程是( )m.
如图,有一圆锥形粮堆,其正视图是边长为6m的正三角形ABC,粮堆母线AC的中点P处有一老鼠正在偷吃粮食,此时,小猫正在B处,它要沿圆锥侧面到达P处捕捉老鼠,则小猫所经过的最短路程是( )m.| A. | 3 | B. | 3$\sqrt{3}$ | C. | 3$\sqrt{5}$ | D. | 4 |
分析 求这只小猫经过的最短距离的问题首先应转化为圆锥的侧面展开图的问题,转化为平面上两点间的距离的问题.根据圆锥的轴截面是边长为6cm的等边三角形可知,展开图是半径是6的半圆.点B是半圆的一个端点,而点P是平分半圆的半径的中点,根据勾股定理就可求出两点B和P在展开图中的距离,就是这只小猫经过的最短距离.
解答 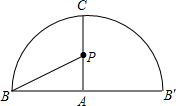 解:圆锥的底面周长是6π,则6π=$\frac{nπ×6}{180}$,
解:圆锥的底面周长是6π,则6π=$\frac{nπ×6}{180}$,
∴n=180°,即圆锥侧面展开图的圆心角是180度.
则在圆锥侧面展开图中AP=3,AB=6,∠BAP=90度.
∴在圆锥侧面展开图中BP=$\sqrt{{3}^{2}+{6}^{2}}$m.
故小猫经过的最短距离是3$\sqrt{5}$m.
故选C.
点评 本题考查的是平面展开-最短路线问题,根据题意画出圆锥的侧面展开图,利用勾股定理求解是解答此题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | -$\frac{3}{2}$ | C. | -$\frac{2}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
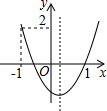 如图,二次函数y=ax2+bx+c的图象开口向上,图象经过点(-1,2)和(1,0),且与y轴相交于负半轴,给出四个结论:①abc<0;②2a+b>0;③a+c=1;④a>1;⑤3a+2b<-1.其中正确结论的序号是②③④.
如图,二次函数y=ax2+bx+c的图象开口向上,图象经过点(-1,2)和(1,0),且与y轴相交于负半轴,给出四个结论:①abc<0;②2a+b>0;③a+c=1;④a>1;⑤3a+2b<-1.其中正确结论的序号是②③④.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
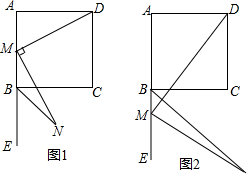
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com