
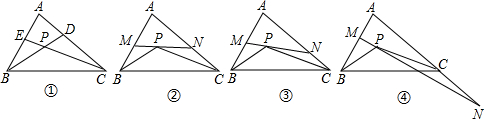
分析 (1)运用三角形的内角和定理及角平分线的定义,首先求出∠1+∠2,进而求出∠BPC即可解决问题.
(2)运用(1)中的结论,结合三角形的内角和定理逐一分类解析,即可解决问题.
解答 解:(1)如图①∵在△ABC中,∠A+∠B+∠ACB=180°,且∠A=80°,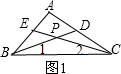
∴∠ABC+∠ACB=100°,
∵∠1=$\frac{1}{2}$∠ABC,∠2=$\frac{1}{2}$∠ACB,
∴∠1+∠2=$\frac{1}{2}$(∠ABC+∠ACB)=$\frac{1}{2}$×100°=50°,
∴∠BPC=180°-(∠1+∠2)=180°-50°=130°.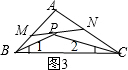
(2)(ⅰ)如图③,由(1)知:∠BPC=180°-(∠1+∠2);
∵∠1+∠2=$\frac{1}{2}$(180°-∠A)=90°$-\frac{1}{2}$∠A,
∴∠BPC=180°-(90°-$\frac{1}{2}$∠A)=90°+$\frac{1}{2}$∠A;
∴∠MPB+∠NPC=180°-∠BPC=180°-(90°+$\frac{1}{2}$∠A)=90°-$\frac{1}{2}$∠A.
(ⅱ)不成立,∠MPB-∠NPC=90°-$\frac{1}{2}$∠A.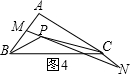
如图④,由(ⅰ)知:∠BPC=90°+$\frac{1}{2}$∠A,
∴∠MPB-∠NPC=180°-∠BPC
=180°-(90°+$\frac{1}{2}$∠A)
=90°-$\frac{1}{2}$∠A.
点评 该题主要考查了三角形的内角和定理、角平分线的定义等几何知识点及其应用问题;牢固掌握三角形的内角和定理、角平分线的定义等几何知识点是基础,灵活运用是关键.


科目:初中数学 来源: 题型:解答题
 如图,正方形ABCD的对角线相交于点O,点E,F分别在OA,OB上,且OE=OF,BE和CF有特殊的大小关系吗?BE和CF有特殊的位置关系吗?证明你的结论.
如图,正方形ABCD的对角线相交于点O,点E,F分别在OA,OB上,且OE=OF,BE和CF有特殊的大小关系吗?BE和CF有特殊的位置关系吗?证明你的结论.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
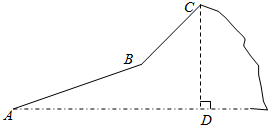 小明春游,登了一座山,地形险峻.由山脚A沿坡角为30°的山坡AB行走480米,到达一个景点B,再由B地沿山坡BC行走360米到达山顶C.如果在山顶C处观测到景点B的俯角为45°,小明在想:山高CD是多少米,你能得出答案吗?(保留$\sqrt{2}$)
小明春游,登了一座山,地形险峻.由山脚A沿坡角为30°的山坡AB行走480米,到达一个景点B,再由B地沿山坡BC行走360米到达山顶C.如果在山顶C处观测到景点B的俯角为45°,小明在想:山高CD是多少米,你能得出答案吗?(保留$\sqrt{2}$)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
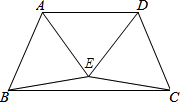 如图,△ABE与△CDE是两个全等的等边三角形,且EA⊥ED.有下列四个结论:(1)∠EBC=15°;(2)AD∥BC;(3)直线CE与AB垂直;(4)四边形ABCD是轴对称图形.其中正确的结论有( )
如图,△ABE与△CDE是两个全等的等边三角形,且EA⊥ED.有下列四个结论:(1)∠EBC=15°;(2)AD∥BC;(3)直线CE与AB垂直;(4)四边形ABCD是轴对称图形.其中正确的结论有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
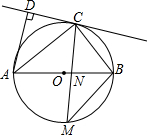 如图,AB是⊙O的直径,点C在⊙O上,AD和过C点的切线互相垂直,垂足为D.
如图,AB是⊙O的直径,点C在⊙O上,AD和过C点的切线互相垂直,垂足为D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com