
【题目】如图,![]() ,
,![]() 平分
平分![]() .
.
(1)如图1,若![]() ,
,
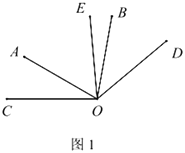
①若![]() ,则
,则![]() 的度数为______(直接写出结果);
的度数为______(直接写出结果);
②求![]() 的度数;
的度数;
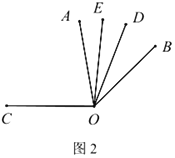
(2)将图1中的![]() 绕顶点
绕顶点![]() 顺时针旋转至图2的位置,试探究
顺时针旋转至图2的位置,试探究![]() 和
和![]() 的度数之间的关系,写出你的结论,并说明理由.
的度数之间的关系,写出你的结论,并说明理由.
【答案】(1)15°;(2)15°;(3)![]() ,理由详见解析.
,理由详见解析.
【解析】
(1)①由角的和差求出∠COD=140°,再根据角平分线的定义得出∠AOE=55°,最后根据∠AOE+∠BOE=70°求解即可;
②根据已知求出![]() ,再由角平分线的性质得出
,再由角平分线的性质得出![]() ,最后根据角的和差关系得出
,最后根据角的和差关系得出![]() ;
;
(2)设∠AOE=x,可得∠BOE=α-x,再由角的和差关系得出∠AOC=2(α-x),从而可以得出![]() .
.
(1)①∵α=70°,∠AOB=![]() ∠COD=α,
∠COD=α,
∴∠AOB=70°,∠COD=140°,
∵∠AOC=30°,
∴∠AOD=∠COD-∠AOC=140°-30°=110°,
∵OE平分∠AOD.
∴∠AOE=![]() ∠AOD=
∠AOD=![]() ×110°=55°,
×110°=55°,
∴∠BOE=∠AOB-∠AOE=70°-55°=15°,
故答案为:![]() ;
;
②∵![]() ,
,![]() ,
,
∴![]() ,
,
又![]() 平分
平分![]() .
.
∴![]() ,
,
∴![]() ;
;
(2)![]() ,理由如下:
,理由如下:
∵![]() 平分
平分![]() ,
,
设![]() ,
,
∴![]() ,
,
![]() ,
,
∴![]() .
.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
【题目】某兴趣小组为了了解本校男生参加课外体育锻炼情况,随机抽取本校300名男生进行了问卷调查,统计整理并绘制了如下两幅尚不完整的统计图.

请根据以上信息解答下列问题:
(1)课外体育锻炼情况扇形统计图中,“经常参加”所对应的圆心角的度数为________;
(2)请补全条形统计图;
(3)该校共有1200名男生,请估计全校男生中经常参加课外体育锻炼并且最喜欢的项目是篮球的人数;
(4)小明认为“全校所有男生中,课外最喜欢参加的运动项目是乒乓球的人数约为1200×![]() =108”,请你判断这种说法是否正确,并说明理由.
=108”,请你判断这种说法是否正确,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
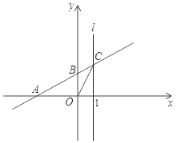
【题目】如图,已知点A(﹣3,0),点B(0,m),直线l:x=1.直线AB与直线l交于点C,连结OC.
(1)△OBC的面积与△OAC的面积比是否是定值?如果是,请求出面积比;如果不是,请说明理由.
(2)若m=2,点T在直线l上且TA=TB,求点T的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】长春市市政工程中需要铺设一条长660米的管道,为了尽量减少施工对城市交通造成的影响,实际施工时,每天铺设管道的长度比原计划增加10%,结果提前6天完成,求实际每天铺设管道的长度与实际施工天数.某同学根据题意列出方程![]() ,则方程中未知数x所表示的量是( )
,则方程中未知数x所表示的量是( )
A. 原计划每天铺设管道的长度 B. 实际每天铺设管道的长度
C. 原计划施工的天数 D. 实际施工的天数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC沿射线BC向右平移到△DCE的位置,连接AD、BD,则下列结论:①AD=BC;②BD、AC互相平分;③四边形ACED是菱形.其中正确的个数是

A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
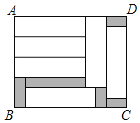
【题目】如图,在长方形ABCD中,放入6个形状和大小都相同的小长方形后,还有一部分空余(阴影部分),已知小长方形的长为a,宽为b,且a>b.
(1)用含a、b的代数式表示长方形ABCD的长AD和宽AB.
(2)用含a、b的代数式表示阴影部分的面积(列式表示即可,不要求化简).
(3)若a=7cm,b=2cm,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
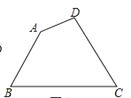
【题目】如图,四边形ABCD中,∠ADB=60°,∠CDB=50°.
(1)若AD∥BC,AB∥CD,求∠ABC的度数;
(2)若∠A=70°,请写出图中平行的线段,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的一元二次方程ax2+bx﹣1=0(a≠0)有一根为x=2019,则一元二次方程a(x﹣1)2+b(x﹣1)=1必有一根为( )
A.![]() B.2020C.2019D.2018
B.2020C.2019D.2018
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,现有一块四边形的木板余料ABCD,经测量AB=25cm,BC=54cm,CD=30cm,且tanB=tanC=![]() ,木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN,则该矩形的面积为____________.
,木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN,则该矩形的面积为____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com