
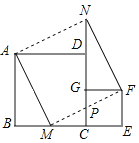
【题目】如图放置的两个正方形,大正方形ABCD边长为a,小正方形CEFG边长为b(a>b),M在边BC上,且BM=b,连AM,MF,MF交CG于点P,将△ABM绕点A旋转至△ADN,将△MEF绕点F旋转至△NGF。给出以下五种结论:∠MAD=∠AND;CP= ![]() ;ΔABM≌ΔNGF;④S四边形AMFN=a2+b2;⑤A,M,P,D四点共线
;ΔABM≌ΔNGF;④S四边形AMFN=a2+b2;⑤A,M,P,D四点共线
其中正确的个数是( )
A. 2 B. 3 C. 4 D. 5
【答案】D
【解析】试题解析:①∵四边形ABCD是正方形,∴∠BAD=∠ADC=∠B=90°,∴∠BAM+∠DAM=90°,∵将△ABM绕点A旋转至△ADN,∴∠NAD=∠BAM,∠AND=∠AMB,∴∠DAM+∠NAD=∠NAD+∠AND=∠AND+∠NAD=90°,∴∠DAM=∠AND,故①正确;
②∵四边形CEFG是正方形,∴PC∥EF,∴△MPC∽△EMF,∴![]() ,∵大正方形ABCD边长为a,小正方形CEFG边长为b(a>b),BM=b,∴EF=b,CM=a﹣b,ME=(a﹣b)+b=a,∴
,∵大正方形ABCD边长为a,小正方形CEFG边长为b(a>b),BM=b,∴EF=b,CM=a﹣b,ME=(a﹣b)+b=a,∴![]() ,∴CP=
,∴CP= ![]() ;故②正确;
;故②正确;
③∵将△MEF绕点F旋转至△NGF,∴GN=ME,∵AB=a,ME=a,∴AB=ME=NG,在△ABM与△NGF中,∵AB=NG=a,∠B=∠NGF=90°,GF=BM=b,∴△ABM≌△NGF;故③正确;
④∵将△ABM绕点A旋转至△ADN,∴AM=AN,∵将△MEF绕点F旋转至△NGF,∴NF=MF,∵△ABM≌△NGF,∴AM=NF,∴四边形AMFN是矩形,∵∠BAM=∠NAD,∴∠BAM+DAM=∠NAD+∠DAN=90°,∴∠NAM=90°,∴四边形AMFN是正方形,∵在Rt△ABM中,a2+b2=AM2,∴S四边形AMFN=AM2=a2+b2;故④正确;
⑤∵四边形AMFN是正方形,∴∠AMP=90°,∵∠ADP=90°,∴∠ABP+∠ADP=180°,∴A,M,P,D四点共圆,故⑤正确.
故选D.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图是![]() 的网格图,请根据要求在网格中完成如下任务:
的网格图,请根据要求在网格中完成如下任务:
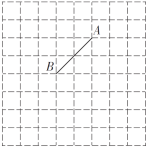
(1)请在网格中建立平面直角坐标系,使点![]() 坐标为
坐标为![]() ,点
,点![]() 坐标为
坐标为![]() ;(要求:画出
;(要求:画出![]() 轴、
轴、![]() 轴,并标出
轴,并标出![]() 、
、![]() 和原点
和原点![]() )
)
(2)以![]() 为一边,在网格中作等腰直角三角形
为一边,在网格中作等腰直角三角形![]() ,找出所有符合条件的
,找出所有符合条件的![]() 点,用
点,用![]() 、
、![]() ……表示,并写出它们的坐标.
……表示,并写出它们的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店经销一种双肩包,已知这种双肩包的成本价为每个30元.市场调查发现,这种双肩包每天的销售量y(单位:个)与销售单价x(单位:元)有如下关系:y=-x+60(30≤x≤60).
设这种双肩包每天的销售利润为w元.
(1)求w与x之间的函数解析式;
(2)这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种双肩包的销售单价不高于48元,该商店销售这种双肩包每天要获得200元的销售利润,销售单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为庆祝中华人民共和国七十周年华诞,某校举行书画大赛,准备购买甲、乙两种文具,奖励在活动中表现优秀的师生已知用300元购买甲种文具的个数是用50元购买乙种文具个数的2倍,购买1个甲种文具比购买1个乙种文具多花费10元.
(1)求购买一个甲种文具、一个乙种文具各需多少元;
(2)若学校计划购买这两种文具共120个,投入资金不多于1000元,且甲种文具至少购买36个,求有多少种购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】半期考试来临,元元到文具店购买考试用的铅笔,签字笔和钢笔,其中铅笔每支8元,签字笔每支l0元,钢笔每支20元,若他一共用了122元,那么他最多能买钢笔_______支.
查看答案和解析>>
科目:初中数学 来源: 题型:
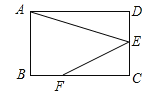
【题目】如图,在矩形ABCD中,点E是CD的中点,点F是BC上一点,且FC=2BF,连接AE,EF.若AB=2,AD=3,则cos∠AEF的值是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,BD为AC的中线,过点C作
,BD为AC的中线,过点C作![]() 于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接 BG,DF.若AF=8,CF=6,则四边形BDFG的周长为_______________.
于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接 BG,DF.若AF=8,CF=6,则四边形BDFG的周长为_______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一块直角三角形的纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( ).

A. 2 cm B. 4 cm C. 3 cm D. 5 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
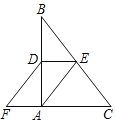
【题目】如图,在Rt△ABC中∠BAC=90°,D,E分别是AB,BC的中点,F在CA的延长线上∠FDA=∠B,AC=6,AB=8,则四边形AEDF的周长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com