
【题目】如图是![]() 的网格图,请根据要求在网格中完成如下任务:
的网格图,请根据要求在网格中完成如下任务:
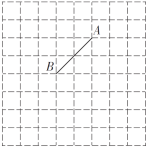
(1)请在网格中建立平面直角坐标系,使点![]() 坐标为
坐标为![]() ,点
,点![]() 坐标为
坐标为![]() ;(要求:画出
;(要求:画出![]() 轴、
轴、![]() 轴,并标出
轴,并标出![]() 、
、![]() 和原点
和原点![]() )
)
(2)以![]() 为一边,在网格中作等腰直角三角形
为一边,在网格中作等腰直角三角形![]() ,找出所有符合条件的
,找出所有符合条件的![]() 点,用
点,用![]() 、
、![]() ……表示,并写出它们的坐标.
……表示,并写出它们的坐标.
【答案】(1)见解析;(2)见解析,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
【解析】
(1)根据点A的坐标,找到坐标原点的位置,然后建立直角坐标系即可;
(2)根据等腰直角三角形腰的情况分类讨论,分别画出对应的图形,即可求出符合要求的点C的坐标.
(1)根据点![]() 坐标为
坐标为![]() ,向下移动2个单位,找到坐标原点O的位置,画出
,向下移动2个单位,找到坐标原点O的位置,画出![]() 轴、
轴、![]() 轴,并标出
轴,并标出![]() 、
、![]() 和原点
和原点![]() ,如下图所示,平面直角坐标系即为所求.
,如下图所示,平面直角坐标系即为所求.
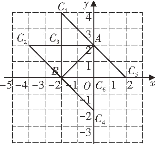
(2)①当等腰直角三角形![]() 是以AC、AB为腰时,如图所示
是以AC、AB为腰时,如图所示
根据勾股定理AC1=AB=![]() ,∠BAC1=45°+45°=90°
,∠BAC1=45°+45°=90°
∴C1符合题意,且![]() ;
;
同理C5符合题意,且![]() ;
;
②当等腰直角三角形![]() 是以BC、BA为腰时,如图所示
是以BC、BA为腰时,如图所示
原理同上:点C2、C4均符合题意,![]() 、
、![]() ;
;
③当等腰直角三角形![]() 是以C为顶点,AC和BC为腰时,如图所示
是以C为顶点,AC和BC为腰时,如图所示
AC3= BC3=2,∠BC3A=90°,
∴C3符合题意,且![]() ;
;
同理C6符合题意,且![]() .
.
综上:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()


科目:初中数学 来源: 题型:
【题目】如图,已知:关于x的二次函数![]() 的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
(1)求二次函数的表达式;
(2)在y轴上是否存在一点P,使△PBC为等腰三角形.若存在,请求出点P的坐标;
(3)有一个点M从点A出发,以每秒1个单位的速度在AB上向点B运动,另一个点N从点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到 达点B时,点M、N同时停止运动,问点M、N运动到何处时,△MNB面积最大,试求出最大面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,四边形ABCD为正方形,点E,F分别在AB与BC上,且∠EDF=45°,易证:AE+CF=EF(不用证明).
(1)如图②,在四边形ABCD中,∠ADC=120°,DA=DC,∠DAB=∠BCD=90°,点E,F分别在AB与BC上,且∠EDF=60°.猜想AE,CF与EF之间的数量关系,并证明你的猜想;
(2)如图③,在四边形ABCD中,∠ADC=2α,DA=DC,∠DAB与∠BCD互补,点E,F分别在AB与BC上,且∠EDF=α,请直接写出AE,CF与EF之间的数量关系,不用证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育运动学校准备在甲、已两位射箭选手中选出成绩比较稳定的一人参加集训,两人各射击了5箭,已知他们的总成绩(单位:环)相同,如下表所示:
第1次 | 第2次 | 第3次 | 第4次 | 第5次 | |
甲成绩 | 9 | 4 | 7 | 4 | 6 |
乙成绩 | 7 | 5 | 7 | a | 7 |
(1)试求出表中a的值;
(2)请你通过计算,从平均数和方差的角度分析,谁将被选中.
[注:平均数x=![]() ;方差
;方差![]() ].
].
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=3x与双曲线y=![]() (k≠0,且x>0)交于点A,点A的横坐标是1.
(k≠0,且x>0)交于点A,点A的横坐标是1.
(1)求点A的坐标及双曲线的解析式;
(2)点B是双曲线上一点,且点B的纵坐标是1,连接OB,AB,求△AOB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一张长方形卡片ABCD放在每格宽度为12mm的横格纸中,恰好四个顶点都在横格线上.已知α=36°,求长方形卡片的周长.
(精确到1mm,参考数据:sin36°≈0.60,cos36°≈0.80,tan36°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某办公楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高3米的影子CE,而当光线与地面夹角是45°时,办公楼顶A在地面上的影子F与墙角C有27米的距离(B,F,C在一条直线上).
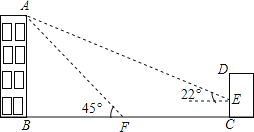
(1)求办公楼AB的高度;
(2)若要在A,E之间挂一些彩旗,请你求出A,E之间的距离.
(参考数据:sin22°≈![]() ,cos22°≈
,cos22°≈![]() ,tan22°≈
,tan22°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+2x+m+1交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列三个判断中:①当x>0时,y>0;②若a=﹣1,则b=4;③抛物线上有两点P(x1,y1)和Q(x2,y2),若x1<1<x2,且x1+x2>2,则y1>y2;正确的是( )
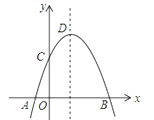
A. ① B. ② C. ③ D. ①②③都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
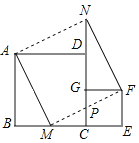
【题目】如图放置的两个正方形,大正方形ABCD边长为a,小正方形CEFG边长为b(a>b),M在边BC上,且BM=b,连AM,MF,MF交CG于点P,将△ABM绕点A旋转至△ADN,将△MEF绕点F旋转至△NGF。给出以下五种结论:∠MAD=∠AND;CP= ![]() ;ΔABM≌ΔNGF;④S四边形AMFN=a2+b2;⑤A,M,P,D四点共线
;ΔABM≌ΔNGF;④S四边形AMFN=a2+b2;⑤A,M,P,D四点共线
其中正确的个数是( )
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com