
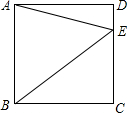
 如图,点E在正方形ABCD的边CD上.若△ABE的面积为8,CE=3,则线段BE的长为5.
如图,点E在正方形ABCD的边CD上.若△ABE的面积为8,CE=3,则线段BE的长为5.  名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 8 | B. | 6 | C. | 5 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
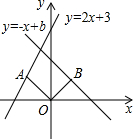 如图,在平面直角坐标系中,点A(-1,m)在直线y=2x+3上,连结OA,将线段OA绕点O顺时针旋转90°,点A的对应点B恰好落在直线y=-x+b上,则b的值为( )
如图,在平面直角坐标系中,点A(-1,m)在直线y=2x+3上,连结OA,将线段OA绕点O顺时针旋转90°,点A的对应点B恰好落在直线y=-x+b上,则b的值为( )| A. | -2 | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
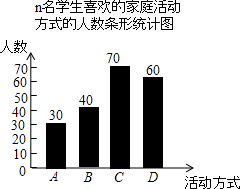 在“世界家庭日”前夕,某校团委随机抽取了n名本校学生,对“世界家庭日”当天所喜欢的家庭活动方式进行问卷调查.问卷中的家庭活动方式包括:
在“世界家庭日”前夕,某校团委随机抽取了n名本校学生,对“世界家庭日”当天所喜欢的家庭活动方式进行问卷调查.问卷中的家庭活动方式包括:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
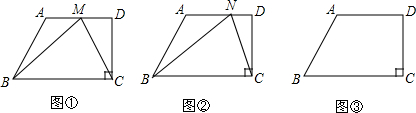
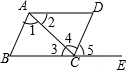 分别根据已知条件进行推理,得出结论,并说明理由.
分别根据已知条件进行推理,得出结论,并说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com