
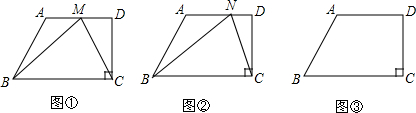
分析 (1)如图①,过A作AE⊥BC,可得出四边形AECD为矩形,得到EC=AD,BE=BC-EC,在直角三角形ABE中,求出AE的长,即为三角形BMC的高,求出三角形BMC面积即可;
(2)如图②,作点C关于直线AD的对称点C′,连接C′N,C′D,C′B交AD于点N′,连接CN′,则BN+NC=BN+NC′≥BC′=BN′+CN′,可得出△BNC周长的最小值为△BN′C的周长=BN′+CN′+BC=BC′+BC,求出即可;
(3)如图③所示,存在点P,使得cos∠BPC的值最小,作BC的中垂线PQ交BC于点Q,交AD于点P,连接BP,CP,作△BPC的外接圆O,圆O与直线PQ交于点N,则PB=PC,圆心O在PN上,根据AD与BC平行,得到圆O与AD相切,根据PQ=DC,判断得到PQ大于BQ,可得出圆心O在BC上方,在AD上任取一点P′,连接P′B,P′C,P′B交圆O于点M,连接MC,可得∠BPC=∠BMC≥∠BP′C,即∠BPC最小,cos∠BPC的值最小,连接OB,求出即可.
解答 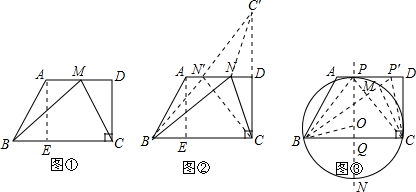 解:(1)如图①,过A作AE⊥BC,
解:(1)如图①,过A作AE⊥BC,
∴四边形AECD为矩形,
∴EC=AD=8,BE=BC-EC=12-8=4,
在Rt△ABE中,∠ABE=60°,BE=4,
∴AB=2BE=8,AE=$\sqrt{{8}^{2}-{4}^{2}}$=4$\sqrt{3}$,
则S△BMC=$\frac{1}{2}$BC•AE=24$\sqrt{3}$;
故答案为:24$\sqrt{3}$;
(2)如图②,作点C关于直线AD的对称点C′,连接C′N,C′D,C′B交AD于点N′,连接CN′,则BN+NC=BN+NC′≥BC′=BN′+CN′,
∴△BNC周长的最小值为△BN′C的周长=BN′+CN′+BC=BC′+BC,
∵AD∥BC,AE⊥BC,∠ABC=60°,
∴过点A作AE⊥BC,则CE=AD=8,
∴BE=4,AE=BE•tan60°=4$\sqrt{3}$,
∴CC′=2CD=2AE=8$\sqrt{3}$,
∵BC=12,
∴BC′=$\sqrt{B{C}^{2}+CC{′}^{2}}$=4$\sqrt{21}$,
∴△BNC周长的最小值为4$\sqrt{21}$+12;
(3)如图③所示,存在点P,使得cos∠BPC的值最小,
作BC的中垂线PQ交BC于点Q,交AD于点P,连接BP,CP,作△BPC的外接圆O,圆O与直线PQ交于点N,则PB=PC,圆心O在PN上,
∵AD∥BC,
∴圆O与AD相切于点P,
∵PQ=DC=4$\sqrt{3}$>6,
∴PQ>BQ,
∴∠BPC<90°,圆心O在弦BC的上方,
在AD上任取一点P′,连接P′B,P′C,P′B交圆O于点M,连接MC,
∴∠BPC=∠BMC≥∠BP′C,
∴∠BPC最大,cos∠BPC的值最小,
连接OB,则∠BON=2∠BPN=∠BPC,
∵OB=OP=4$\sqrt{3}$-OQ,
在Rt△BOQ中,根据勾股定理得:OQ2+62=(4$\sqrt{3}$-OQ)2,
解得:OQ=$\frac{\sqrt{3}}{2}$,
∴OB=$\frac{7\sqrt{3}}{2}$,
∴cos∠BPC=cos∠BOQ=$\frac{OQ}{OB}$=$\frac{1}{7}$,
则此时cos∠BPC的值为$\frac{1}{7}$.
点评 此题属于四边形综合题,涉及的知识有:勾股定理,矩形的判定与性质,对称的性质,圆的切线的判定与性质,以及锐角三角函数定义,熟练掌握定理及性质是解本题的关键.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:解答题
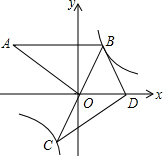 如图,在平面直角坐标系中,∠AOB=90°,AB∥x轴,OB=2,双曲线y=$\frac{k}{x}$经过点B,将△AOB绕点B逆时针旋转,使点O的对应点D落在x轴的正半轴上.若AB的对应线段CB恰好经过点O.
如图,在平面直角坐标系中,∠AOB=90°,AB∥x轴,OB=2,双曲线y=$\frac{k}{x}$经过点B,将△AOB绕点B逆时针旋转,使点O的对应点D落在x轴的正半轴上.若AB的对应线段CB恰好经过点O.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
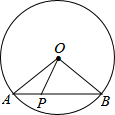 如图,⊙O的半径是2,AB是⊙O的弦,点P是弦AB上的动点,且1≤OP≤2,则弦AB所对的圆周角的度数是( )
如图,⊙O的半径是2,AB是⊙O的弦,点P是弦AB上的动点,且1≤OP≤2,则弦AB所对的圆周角的度数是( )| A. | 60° | B. | 120° | C. | 60°或120° | D. | 30°或150° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
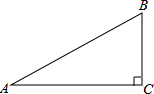 如图,有一滑梯AB,其水平宽度AC为5.3米,铅直高度BC为2.8米,则∠A的度数约为27.8°(用科学计算器计算,结果精确到0.1°).
如图,有一滑梯AB,其水平宽度AC为5.3米,铅直高度BC为2.8米,则∠A的度数约为27.8°(用科学计算器计算,结果精确到0.1°).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
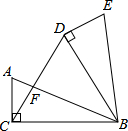 如图,在Rt△ABC中,∠ACB=90°,AC=5cm,BC=12cm,将△ABC绕点B顺时针旋转60°,得到△BDE,连接DC交AB于点F,则△ACF与△BDF的周长之和为42cm.
如图,在Rt△ABC中,∠ACB=90°,AC=5cm,BC=12cm,将△ABC绕点B顺时针旋转60°,得到△BDE,连接DC交AB于点F,则△ACF与△BDF的周长之和为42cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com