
【题目】如图,∠1=∠2,∠C=∠D,AC、BD交于E点,下列结论中不正确的是( ) 
A.∠DAE=∠CBE
B.△DEA不全等于△CEB
C.CE=DE
D.△EAB是等腰三角形
【答案】B
【解析】解:∵∠1+∠C+∠ABC=∠2+∠D+∠DAB=180°,且∠1=∠2,∠C=∠D, ∴∠ABC=∠DAB,
∴∠ABC﹣∠2=∠DAB﹣∠1,
∴∠DAB=∠CBA.故A正确;
在△DEA和△CEB中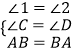 ,
,
∴△DEA≌△CEB(AAS),故B错误;
∴AC=BD.
∵∠1=∠2,
∴BE=AE,
∴△EAB是等腰三角形,AC﹣AE=BD﹣BE,故D正确;
∴CE=DE.故C正确.
故选B.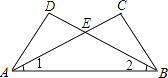
根据三角形的内角和定理就可以求出∠DAB=∠CBA,由等式的性质就可以得出∠DAE=∠CBE,根据AAS就可以得出△DEA≌△CEB;由△DEA≌△CEB就可以得出CE=DE,∠1=∠2就可以得出AE=BE,就可以得出结论.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】同学们做足球操时,为了保证一队同学站成一条直线,先让两个同学站好不动,其他同学依次往后站,要求目视前方只能看到各自前面的那个同学,这种做法用几何知识解释应是( )
A. 两点之间,线段最短 B. 射线只有一个端点
C. 两点确定一条直线 D. 两直线相交只有一个交点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区在一次九年级数学做了检测中,有一道满分8分的解答题,按评分标准,所有考生的得分只有四种:0分,3分,5分,8分.老师为了了解学生的得分情况与题目的难易情况,从全区4500名考生的试卷中随机抽取一部分,通过分析与整理,绘制了如下两幅图不完整的统计图.
请根据以上信息解答下列问题:
(1)填空:a= ,b= ,并把条形统计图补全;
(2)请估计该地区此题得满分(即8分)的学生人数;
(3)已知难度系数的计算公式为L=![]() ,其中L为难度系数,X为样本平均得分,W为试题满分值.一般来说,根据试题的难度系数可将试题分为以下三类:当0<L≤0.4时,此题为难题;当0.4<L≤0.7时,此题为中等难度试题;当0.7<L<1时,此题为容易题.试问此题对于该地区的九年级学生来说属于哪一类?
,其中L为难度系数,X为样本平均得分,W为试题满分值.一般来说,根据试题的难度系数可将试题分为以下三类:当0<L≤0.4时,此题为难题;当0.4<L≤0.7时,此题为中等难度试题;当0.7<L<1时,此题为容易题.试问此题对于该地区的九年级学生来说属于哪一类?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A、B两地相距40km,甲、乙两人沿同一公路从A地出发到B地,甲骑摩托车,乙骑自行车,图中CD、OE分别表示甲、乙离开A地的路程y(km)与时间x(h)的函数关系的图象,结合图象解答下列问题. 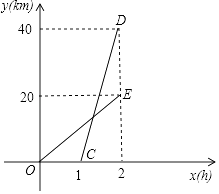
(1)甲比乙晚出发小时,乙的速度是km/h;
(2)在甲出发后几小时,两人相遇?
(3)甲到达B地后,原地休息0.5小时,从B地以原来的速度和路线返回A地,求甲在返回过程中与乙相距10km时,对应x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+![]() 与x轴交于A(-3,0),B(1,0)两点,与y轴交于点C,点D与点C关于抛物线的对称轴对称.
与x轴交于A(-3,0),B(1,0)两点,与y轴交于点C,点D与点C关于抛物线的对称轴对称.
(1)求抛物线的解析式,并直接写出点D的坐标;
(2)如图1,点P从点A出发,以每秒1个单位长度的速度沿A→B匀速运动,到达点B时停止运动.以AP为边作等边△APQ(点Q在x轴上方).设点P在运动过程中,△APQ与四边形AOCD重叠部分的面积为S,点P的运动时间为t秒,求S与t之间的函数关系式;
(3)如图2,连接AC,在第二象限内存在点M,使得以M、O、A为顶点的三角形与△AOC相似.请直接写出所有符合条件的点M坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法错误的是( )
A. 对顶角相等 B. 两点之间所有连线中,线段最短
C. 等角的补角相等 D. 过任意一点P,都能画一条直线与已知直线平行
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com