
【题目】如图①点A,B,C,D在同一直线上,AB=CD,作CE⊥AD,BF⊥AD,且AE=DF. 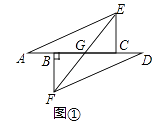
(1)证明:EF平分线段BC;
(2)若△BFD沿AD方向平移得到图②时,其他条件不变,(1)中的结论是否仍成立?请说明理由. 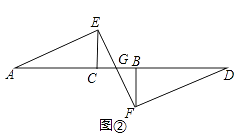
【答案】
(1)证明:∵CE⊥AD,BF⊥AD,
∴∠ACE=∠DBF=90°,
∵AB=CD,
∴AB+BC=BC+CD,即AC=DB,
在Rt△ACE和Rt△DBF中,
![]() ,
,
∴Rt△ACE≌Rt△DBF(HL),
∴CE=FB,
在△CEG和△BFG中,
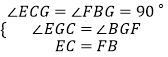 ,
,
∴△CEG≌△BFG(AAS),
∴CG=BG,即EF平分线段BC;
(2)(1)中结论成立,理由为:
证明:∵CE⊥AD,BF⊥AD,
∴∠ACE=∠DBF=90°,
∵AB=CD,
∴AB﹣BC=CD﹣BC,即AC=DB,
在Rt△ACE和Rt△DBF中,
![]() ,
,
∴Rt△ACE≌Rt△DBF(HL),
∴CE=FB,
在△CEG和△BFG中,
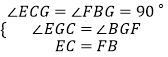 ,
,
∴△CEG≌△BFG(AAS),
∴CG=BG,即EF平分线段BC.
【解析】(1)由AB=CD,利用等式的性质得到AC=BD,再由AE=DF,利用HL得到直角三角形ACE与直角三角形DBF全等,利用全等三角形对应边相等得到EC=BF,再利用AAS得到三角形ECG与三角形FBG全等,利用全等三角形对应边相等得到BG=CG,即可得证;(2)(1)中的结论成立,理由为:由AC=DB,利用等式的性质得到AC=BD,再由AE=DF,利用HL得到直角三角形ACE与直角三角形DBF全等,利用全等三角形对应边相等得到EC=BF,再利用AAS得到三角形ECG与三角形FBG全等,利用全等三角形对应边相等得到BG=CG,即可得证.
【考点精析】通过灵活运用平移的性质,掌握①经过平移之后的图形与原来的图形的对应线段平行(或在同一直线上)且相等,对应角相等,图形的形状与大小都没有发生变化;②经过平移后,对应点所连的线段平行(或在同一直线上)且相等即可以解答此题.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里装有除颜色外都相同的5个白球和若干个红球,在不允许将球倒出来数的前提下,小亮为了估计其中的红球数,采用如下方法:先将口袋中的球摇匀,再从口袋里随机摸出一球,记下颜色,然后把它放回口袋中,不断重复上述过程,小亮共摸了100次,其中有10次摸到白球.因此小亮估计口袋中的红球大约有( )个.
A.45
B.48
C.50
D.55
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O为直线AB上一点,∠AOC=110°,OM平分∠AOC,∠MON=90° 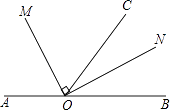
(1)求∠BOM的度数;
(2)ON是∠BOC的角平分线吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a,b,c在数轴上的位置如图所示,所对应的点分别为A,B,C. ![]()
(1)填空:A,B之间的距离为 , B,C之间的距离为 , A,C之间的距离为;
(2)化简:|a+b|﹣|c﹣b|+|b﹣a|;
(3)a、b、c在数轴上的位置如图所示,且c2=4,﹣b的倒数是它本身,a的绝对值的相反数是﹣2,求﹣a+2b﹣c﹣2(a﹣4c﹣b)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题引入】
已知:如图BE、CF是ΔABC的中线,BE、CF相交于G。求证: ![]()
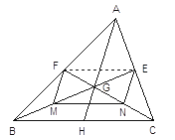
证明:连结EF
∵E、F分别是AC、AB的中点
∴EF∥BF且EF=![]() BC
BC
∴![]()
【思考解答】
(1)连结AG并延长AG交BC于H,点H是否为BC中点 (填“是”或“不是”)
(2)①如果M、N分别是GB、GC的中点,则四边形EFMN 是 四边形。
②当![]() 的值为 时,四边形EFMN 是矩形。
的值为 时,四边形EFMN 是矩形。
③当![]() 的值为 时,四边形EFMN 是菱形。
的值为 时,四边形EFMN 是菱形。
④如果AB=AC,且AB=10,BC=16,则四边形EFMN的面积![]() =_________
=_________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司产销一种产品,为保证质量,每个周期产销商品件数控制在100以内,产销成本C是商品件数x的二次函数,调查数据如表:
产销商品件数(x/件) | 10 | 20 | 30 |
产销成本(C/元) | 120 | 180 | 260 |
商品的销售价格(单位:元)为P=35﹣![]() x(每个周期的产销利润=Px﹣C)
x(每个周期的产销利润=Px﹣C)
(1)直接写出产销成本C与商品件数x的函数关系式(不要求写出自变量的取值范围)
(2)该公司每个周期产销多少件商品时,利润达到220元?
(3)求该公司每个周期的产销利润的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com