
【题目】【问题引入】
已知:如图BE、CF是ΔABC的中线,BE、CF相交于G。求证: ![]()
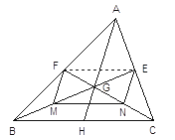
证明:连结EF
∵E、F分别是AC、AB的中点
∴EF∥BF且EF=![]() BC
BC
∴![]()
【思考解答】
(1)连结AG并延长AG交BC于H,点H是否为BC中点 (填“是”或“不是”)
(2)①如果M、N分别是GB、GC的中点,则四边形EFMN 是 四边形。
②当![]() 的值为 时,四边形EFMN 是矩形。
的值为 时,四边形EFMN 是矩形。
③当![]() 的值为 时,四边形EFMN 是菱形。
的值为 时,四边形EFMN 是菱形。
④如果AB=AC,且AB=10,BC=16,则四边形EFMN的面积![]() =_________
=_________
科目:初中数学 来源: 题型:
【题目】如图①点A,B,C,D在同一直线上,AB=CD,作CE⊥AD,BF⊥AD,且AE=DF. 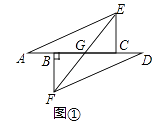
(1)证明:EF平分线段BC;
(2)若△BFD沿AD方向平移得到图②时,其他条件不变,(1)中的结论是否仍成立?请说明理由. 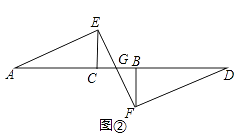
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市有甲、乙两种出租车,他们的服务质量相同.甲的计价方式为:当行驶路程不超过3千米时收费10元,每超过1千米则另外收费1.2元(不足1千米按1千米收费);乙的计价方式为:当行驶路程不超过3千米时收费8元,每超过1千米则另外收费1.8元(不足1千米按1千米收费).某人到该市出差,需要乘坐的路程为x千米.
(1)当x=5时,请分别求出乘坐甲、乙两种出租车的费用;
(2)用代数式表示此人分别乘坐甲、乙出租车各所需要的费用;
(3)假设此人乘坐的路程为13千米多一点,请问他乘坐哪种车较合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知今年小明的年龄是x岁,小红的年龄比小明的2倍少4岁,小华的年龄比小红的 ![]() 还大1岁,小刚的年龄恰好为小明、小红、小华三个人年龄的和.试用含x的式子表示小刚的年龄,并计算当x=5时小刚的年龄.
还大1岁,小刚的年龄恰好为小明、小红、小华三个人年龄的和.试用含x的式子表示小刚的年龄,并计算当x=5时小刚的年龄.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是( )

A. 5![]() B. 25 C. 10
B. 25 C. 10![]() +5 D. 35
+5 D. 35
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com