
【题目】填空:把下面的推理过程补充完整,并在括号内注明理由.
已知:如图,△ABC中,D、E分别为AB、AC的中点,过点C作CF//AB交DE的延长线于F.求证:AB=2CF.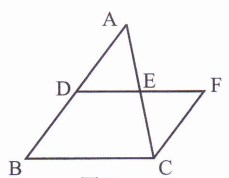
证明:∵CF//AB(已知),
∴∠ADE=∠F( ![]() ),
),
∵E为AC的中点(已知),
∴AE=CE(中点的定义).
在△ADE与△CFE中,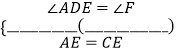
∴△ADE△CFE( ![]() )
)
∴AD=CF( ![]() )
)
∵D为AB的中点
∴AB=2AD(中点的定义)
∴AB=2CF(等量代换)
【答案】解:证明:∵ CF//AB(已知)
∴∠ADE=∠F( 两直线平行,内错角相等 )
∵E为AC的中点(已知)
∴AE=CE(中点的定义)
在△ADE与△CFE中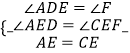 ( 对顶角相等 )
( 对顶角相等 )
∴△ADE≌△CFE( AAS )
∴AD=CF(全等三角形的对应边相等)
∵D为AB的中点
∴AB=2AD(中点的定义)
∴AB=2CF(等量代换)
【解析】证明题中每一步要求做到有理有据的,条理清晰;根据解题步骤给出的条件和结论,找它的“有关的定义和定理”填在空里即可.
【考点精析】解答此题的关键在于理解平行线的性质的相关知识,掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D、E分别为AB、AC上两点,将△ABC沿直线DE折叠,使得点A落在△ABC右侧的A1处,则∠A、∠1、∠2之间满足的关系式是( )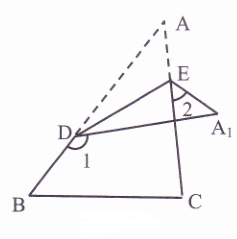
A.∠A=∠1-∠2
B.∠A= ![]() ∠1-∠2
∠1-∠2
C.∠A=∠1-2∠2
D.2∠A=∠1-∠2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若a是有理数,则计算正确的是( )
A. (﹣a)+(﹣a)=2a B. ﹣a+(﹣a)=0
C. (﹣a)﹣(﹣a)=2a D. ﹣a﹣(+a)=﹣2a
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】人的大脑所能记忆的内容是有限的,随着时间的推移,记忆的东西会逐渐遗忘.为提升记忆的效果,需要有计划的按时复习巩固.图中的实线部分是记忆保持量(%)与时间(天)之间的关系图.请根据图回答下列问题: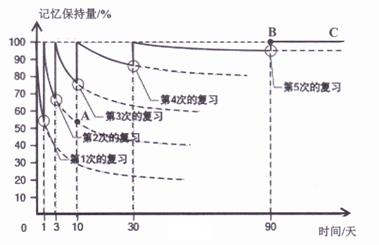
(1)图中的自变量是 , 应变量是;
(2)如果不复习,3天后记忆保持量约为;
(3)图中点A表示的意义是;
(4)图中射线BC表示的意义是;
(5)经过第1次复习与不进行复习,3天后记忆保持量相差约为;
(6)10天后,经过第2次复习与从来都没有复习的记忆保持量相差约为.
查看答案和解析>>
科目:初中数学 来源: 题型:
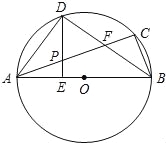
【题目】已知:如图,△ABC内接于⊙O,AB为直径,∠CBA的平分线交AC于点F,交⊙O于点D,DE⊥AB于点E,且交AC于点P,连结AD.
(1)求证:∠DAC=∠DBA;
(2)求证:P是线段AF的中点;
(3)连接CD,若CD﹦3,BD﹦4,求⊙O的半径和DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com