
【题目】如图,这是一幅2018年俄罗斯世界杯的长方形宣传画,长为4m,宽为2m.为测量画上世界杯图案的面积,现将宣传画平铺在地上,向长方形宣传画内随机投掷骰子(假设骰子落在长方形内的每一点都是等可能的),经过大量重复投掷试验,发现骰子落在世界杯图案中的频率稳定在常数0.4左右.由此可估计宣传画上世界杯图案的面积为____.

科目:初中数学 来源: 题型:
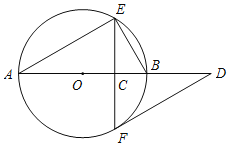
【题目】如图,AB是⊙O的直径,弦EF⊥AB于点C,过点F作⊙O的切线交AB的延长线于点D.
(1)已知∠A=α,求∠D的大小(用含α的式子表示);
(2)取BE的中点M,连接MF,请补全图形;若∠A=30°,MF=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点D在AB的延长线上,C、E是⊙O上的两点,CE=CB,∠BCD=∠CAE,延长AE交BC的延长线于点F.
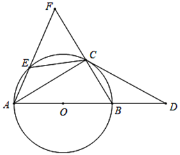
求证:(1)CD是⊙O的切线;
(2)CE=CF;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知抛物线y=![]() x2+bx+c与x轴交于A(﹣1,0),B(2,0)两点,与y轴交于点C.
x2+bx+c与x轴交于A(﹣1,0),B(2,0)两点,与y轴交于点C.
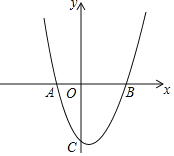
(1)求该抛物线的解析式及点C的坐标;
(2)直线y=﹣x﹣2与该抛物线在第四象限内交于点D,与x轴交于点F,连接AC,CD,线段AC与线段DF交于点G,求证:△AGF≌△CGD;
(3)直线y=m(m>0)与该抛物线的交点为M,N(点M在点N的左侧),点M关于y轴的对称点为点M′,点H的坐标为(1,0),若四边形NHOM′的面积为![]() ,求点H到OM′的距离d.
,求点H到OM′的距离d.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市将实行居民生活用电阶梯电价方案,如下表,图中折线反映了每户居民每月电费![]() (元)与用电量
(元)与用电量![]() (度)间的函数关系.
(度)间的函数关系.
档次 | 第一档 | 第二档 | 第三档 |
每月用电量 |
|
|
|
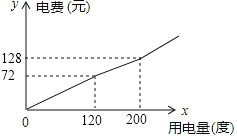
(1)小王家某月用电![]() 度,需交电费___________元;
度,需交电费___________元;
(2)求第二档电费![]() (元)与用电量
(元)与用电量![]() (度)之间的函数关系式;
(度)之间的函数关系式;
(3)小王家某月用电![]() 度,交纳电费
度,交纳电费![]() 元,请你求出第三档每度电费比第二档每度电费多多少元?
元,请你求出第三档每度电费比第二档每度电费多多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是由边长为1的小正方形组成的8×4网格,每个小正方形的顶点叫做格点,点A,B,C,D均在格点上,在网格中将点D按下列步骤移动;
第一步:点D绕点A顺时针旋转180°得到点D1;
第二步:点D1绕点B顺时针旋转90°得到点D2;
第三步:点D2绕点C顺时针旋转90°回到点D.
(1)请用圆规画出点D→D1→D2→D经过的路径;
(2)求所画图形的周长(结果保留π);
(3)求所画图形的面积(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了预防疾病,某单位对办公室采用药熏消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成为正比例,药物燃烧后,y与x成反比例(如图),现测得药物8分钟燃毕,此时室内空气中每立方米的含药量6毫克,请根据题中所提供的信息,解答下列问题:

(1)药物燃烧时,y关于x的函数关系式为________,自变量x的取值范为________;药物燃烧后,y关于x的函数关系式为________.
(2)研究表明,当空气中每立方米的含药量低于1.6毫克时员工方可进办公室,那么从消毒开始,至少需要经过________分钟后,员工才能回到办公室;
(3)研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市对今年“元旦”期间销售A、B、C三种品牌的绿色鸡蛋情况进行了统计,并绘制如图所示的扇形统计图和条形统计图.根据图中信息解答下列问题:
(1)该超市“元旦”期间共销售 个绿色鸡蛋,A品牌绿色鸡蛋在扇形统计图中所对应的扇形圆心角是 度;
(2)补全条形统计图;
(3)如果该超市的另一分店在“元旦”期间共销售这三种品牌的绿色鸡蛋1500个,请你估计这个分店销售的B种品牌的绿色鸡蛋的个数?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形![]() 中,
中,![]() ,点
,点![]() 从点
从点![]() 出发向点
出发向点![]() 移动,速度为每秒1个单位长度,点
移动,速度为每秒1个单位长度,点![]() 从点
从点![]() 出发向点
出发向点![]() 移动,速度为每秒2个单位长度. 两点同时出发,且其中的任何一点到达终点后,另一点的移动同时停止.
移动,速度为每秒2个单位长度. 两点同时出发,且其中的任何一点到达终点后,另一点的移动同时停止.
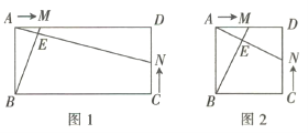
(1)若两点的运动时间为![]() ,当
,当![]() 为何值时,
为何值时,![]() ?
?
(2)在(1)的情况下,猜想![]() 与
与![]() 的位置关系并证明你的结论.
的位置关系并证明你的结论.
(3)①如图2,当![]() 时,其他条件不变,若(2)中的结论仍成立,则
时,其他条件不变,若(2)中的结论仍成立,则![]() _________.
_________.
②当![]() ,
,![]() 时,其他条件不变,若(2)中的结论仍成立,则
时,其他条件不变,若(2)中的结论仍成立,则![]() _________(用含
_________(用含![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com