
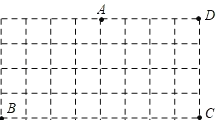
【题目】如图是由边长为1的小正方形组成的8×4网格,每个小正方形的顶点叫做格点,点A,B,C,D均在格点上,在网格中将点D按下列步骤移动;
第一步:点D绕点A顺时针旋转180°得到点D1;
第二步:点D1绕点B顺时针旋转90°得到点D2;
第三步:点D2绕点C顺时针旋转90°回到点D.
(1)请用圆规画出点D→D1→D2→D经过的路径;
(2)求所画图形的周长(结果保留π);
(3)求所画图形的面积(结果保留π).
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,一只箱子沿着斜面向上运动,箱高AB=1.3cm,当BC=2.6m时,点B离地面的距离BE=1m,则此时点A离地面的距离是( )
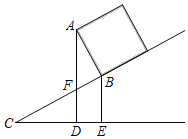
A.2.2mB.2mC.1.8mD.1.6m
查看答案和解析>>
科目:初中数学 来源: 题型:
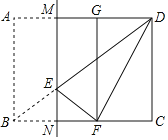
【题目】如图,在矩形ABCD中,AB:BC=3:4,点E是对角线BD上一动点(不与点B,D重合),将矩形沿过点E的直线MN折叠,使得点A,B的对应点G,F分别在直线AD与BC上,当△DEF为直角三角形时,CN:BN的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD是△ABC的角平分线,点E,F分别在BC,AB上,且DE∥AB,BE=AF.
(1)求证:四边形ADEF是平行四边形;
(2)若∠ABC=60°,BD=6,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,这是一幅2018年俄罗斯世界杯的长方形宣传画,长为4m,宽为2m.为测量画上世界杯图案的面积,现将宣传画平铺在地上,向长方形宣传画内随机投掷骰子(假设骰子落在长方形内的每一点都是等可能的),经过大量重复投掷试验,发现骰子落在世界杯图案中的频率稳定在常数0.4左右.由此可估计宣传画上世界杯图案的面积为____.

查看答案和解析>>
科目:初中数学 来源: 题型:
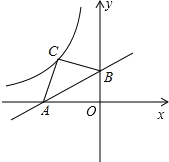
【题目】直线y=![]() x+3与两坐标轴交于A、B两点,以AB为斜边在第二象限内作等腰Rt△ABC,反比例函数y=
x+3与两坐标轴交于A、B两点,以AB为斜边在第二象限内作等腰Rt△ABC,反比例函数y=![]() (x<0)的图象过点C,则m=_____.
(x<0)的图象过点C,则m=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家饮水机中原有水的温度为20℃,通电开机后,饮水机自动开始加热(此过程中水温y(℃)与开机时间x(分)满足一次函数关系),当加热到100℃时自动停止加热,随后水温开始下降,此过程中水温y(℃)与开机时间x(分)成反比例关系,当水温降至20C时,饮水机又自动开始加热…,重复上述程序(如图所示),根据图中提供的信息,解答下列问题:
(1)当0≤x≤8时,求水温y(℃)与开机时间x(分)的函数关系式;
(2)求图中t的值;
(3)若小明上午八点将饮水机在通电开机(此时饮水机中原有水的温度为20℃后即外出散步,预计上午八点半散步回到家中,回到家时,他能喝到饮水机内不低于30℃的水吗?请说明你的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
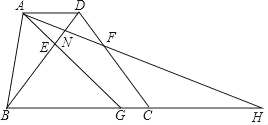
【题目】如图,在梯形ABCD中,AD∥BC,BC=18,DB=DC=15,点E、F分别在线段BD、CD上,DE=DF=5.AE的延长线交边BC于点G,AF交BD于点N、其延长线交BC的延长线于点H.
(1)求证:BG=CH;
(2)设AD=x,△ADN的面积为y,求y关于x的函数解析式,并写出它的定义域;
(3)联结FG,当△HFG与△ADN相似时,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
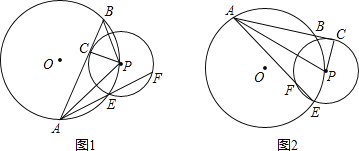
【题目】如图,P是⊙O上的一个点,⊙P与⊙O的一个交点是E,⊙O的弦AB(或延长线)与⊙P相切,C是切点,AE(或延长线)交⊙P于点F,连接PA、PB,设⊙O的半径为R,⊙P的半径为r(R>r),
(1)如图1,求证:PAPB=2rR;
(2)如图2,当切点C在⊙O的外部时,(1)中的结论是否成立,试证明之;
(3)探究(图2)已知PA=10,PB=4,R=2r,求EF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com