练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

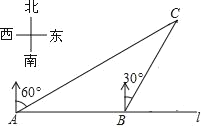
    【题目】如图，在一笔直的海岸线l上有相距2km的A，B两个观测站，B站在A站的正东方向上，从A站测得船C在北偏东60°的方向上，从B站测得船C在北偏东30°的方向上，则船C到海岸线l的距离为多少千米？（参考数据：≈1.732，结果保留小数点后一位）

    【答案】船C到海岸线l的距离约为1.7km．

    【解析】

    首先由题意可证得：△ACB是等腰三角形，即可求得BC的长，然后在Rt△CBD中，CD=BCsin60°，求得答案．

    解：过点C作CD⊥AB于点D，根据题意得：∠CAD=90°﹣60°=30°，∠CBD=90°﹣30°=60°，∴∠ACB=∠CBD﹣∠CAD=30°，∴∠CAB=∠ACB，∴BC=AB=2km，在Rt△CBD中，CD=BCsin60°=2×=≈1.7（km），答：船C到海岸线l的距离约为1.7km．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，矩形的顶点在反比例函数的图象上，且，.若动点从开始沿向以每秒1个单位长度的速度运动，同时动点从开始沿向以每秒2个单位长度的速度运动，当其中一个动点到达端点时，另一个动点随之停止运动，设运动时间为秒.

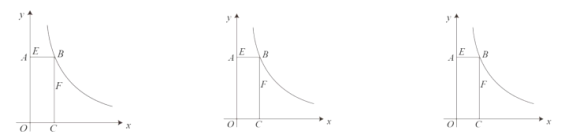
    （1）求反比例函数的表达式；

    （2）当时，在轴上存在点，使的周长最小，请求出此时点的坐标，并直接写出的周长最小值；

    （3）在双曲线上是否存在一点，使以点，，，为顶点的四边形是平行四边形？若存在，请直接写出满足条件的值；若不存在，请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

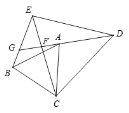
    【题目】如图，已知△ABC和△DCE是等边三角形，连接BE，连接DA并延长交CE于点F，交BE于点G，CD=6，EF=2，那么EG的长为__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在矩形ABCD中，AB＝3，AD＝8，O为AD中点，P是线段AO上一动点，以O为圆心，OP为半径作⊙O分别交BO及BO延长线于点E，F，延长AE交BC于点H．

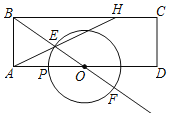
    （1）当OP＝2时，求BH的长．

    （2）当AH交⊙O于另一点G时，连接FG，DF，作DM⊥BF于点M，求证：△EFG∽△FDM．

    （3）连结HO，当△EHO是直角三角形时，求OP的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】对于反比例函数y＝﹣，下列说法错误的是( )

    A.图象分布在第二、四象限

    B.若点A(，)，B(，)都在图象上，且＜，则＜

    C.图象经过点(1，﹣2)

    D.当x＞0时，y随x的增大而增大

    查看答案和解析>>

    科目：初中数学 来源： 题型：

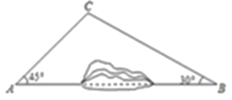
    【题目】为加快城乡对接，建设美丽乡村，某地区对A、B两地间的公路进行改建．如图，A、B两地之间有一座山．汽车原来从A地到B地需途径C地沿折线ACB行驶，现开通隧道后，汽车可直接沿直线AB行驶．已知BC＝100千米，∠A＝45°，∠B＝30°．

    （1）开通隧道前，汽车从A地到B地要走多少千米？

    （2）开通隧道后，汽车从A地到B地可以少走多少千米？（结果保留根号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小慧同学根据学习函数的经验，对函数y＝|x﹣1|的图象与性质进行了探究．下面是小慧的探究过程，请补充完成：

    （1）函数y＝|x﹣1|的自变量x的取值范围是　 　．

    （2）列表，找出y与x的几组对应值．

    x

    …

    ﹣1

    0

    1

    2

    3

    …

    y

    …

    2

    b

    0

    1

    2

    …

    其中，b＝　 　．

    （3）在所给的平面直角坐标系xoy中，描出以上表中各对对应值为坐标的点，并画出该函数的图象；

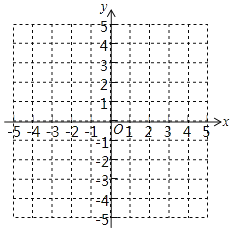
    （4）请根据你画出的函数图象，完成：当x＝﹣5时．y＝　 　．当2012≤|y|≤2019时，x的取值范围是　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，CD是⊙O的切线，点C在直径AB的延长线上．

    （1）求证：∠CAD＝∠BDC；

    （2）若BC＝2，CD＝3，求⊙O的半径．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

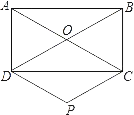
    【题目】已知：如图，在矩形ABCD中，对角线AC与BD相交于点O，过点C，D分别作BD，AC的平行线，两线相交于点P．

    （1）求证：四边形CODP是菱形；

    （2）当矩形ABCD的边AD，DC满足什么关系时，菱形CODP是正方形？请说明理由．

    查看答案和解析>>

    同步练习册答案