
【题目】常用的分解因式的方法有提取公因式法、公式法及十字相乘法,但有更多的多项式只用上述方法就无法分解,如![]() ,我们细心观察这个式子就会发现,前两项符合平方差公式,后两项可提取公因式,前后两部分分别分解因式后会产生公因式,然后提取公因式就可以完成整个式子的分解因式了。过程为:
,我们细心观察这个式子就会发现,前两项符合平方差公式,后两项可提取公因式,前后两部分分别分解因式后会产生公因式,然后提取公因式就可以完成整个式子的分解因式了。过程为:
![]() =
=![]() =
=![]()
这种分解因式的方法叫分组分解法。利用这种方法解决下列问题:
(1)分解因式: ①![]() ;②2x﹣2y﹣x2+y2
;②2x﹣2y﹣x2+y2
(2)![]() 三边a,b,c 满足
三边a,b,c 满足![]() ,判断
,判断![]() 的形状.
的形状.
【答案】(1) (x-y+4)(x-y-4);(2)△ABC的形状是腰和底不相等的等腰三角形或等边三角形,理由见解析
【解析】
试题(1)类比题目中的解题方法可得,将这个多项式的前三项组合,组成完全平方式,利用完全平方公式分解因式,再和第四项利用平方差公式分解因式即可;(2)类比题目中的解题方法可得,将a2﹣ab﹣ac+bc的前两项以及后两项组合,两次利用提取公因式法分解因式可得(a﹣b)(a﹣c),所以(a﹣b)(a﹣c)=0,即可得a=b或a=c,即可判断△ABC的形状.
试题解析:解:(1)x2﹣2xy+y2﹣16
=(x﹣y)2﹣42
=(x﹣y+4)(x﹣y﹣4);
(2)∵a2﹣ab﹣ac+bc=0
∴a(a﹣b)﹣c(a﹣b)=0,
∴(a﹣b)(a﹣c)=0,
∴a=b或a=c,
∴△ABC的形状是等腰三角形.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
【题目】如图,两张宽为1cm的矩形纸条交叉叠放,其中重叠部分部分是四边形ABCD, 
(1)试判断四边形ABCD的形状,并说明理由
(2)若∠BAD=30°,求重叠部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点O在直线AB上,点A1、A2、A3,…在射线OA上,点B1、B2、B3,…在射线OB上,图中的每一个实线段和虚线段的长均为一个单位长度,一个动点M从O点出发,按如图所示的箭头方向沿着实线段和以O为圆心的半圆匀速运动,速度为每秒1个单位长度,按此规律,则动点M到达A101点处所需时间为____秒.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,∠A=30°,DE垂直平分斜边AC,交AB于D,E是垂足,连接CD.若BD=1,则AC的长是( ) 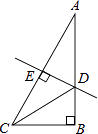
A.2 ![]()
B.2
C.4 ![]()
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于D,CE⊥DE于点E;
(1)若B、C在DE的同侧(如图所示)且AD=CE.求证:AB⊥AC;
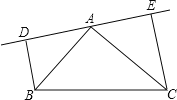
(2)若B、C在DE的两侧(如图所示),其他条件不变,AB与AC仍垂直吗?若是请给出证明;若不是,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:AD与⊙O相切于点D,AF经过圆心与圆交于点E、F,连接DE、DF,且EF=6,AD=4. 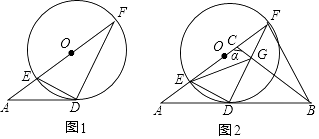
(1)证明:AD2=AEAF;
(2)延长AD到点B,使DB=AD,直径EF上有一动点C,连接CB交DF于点G,连接EG,设∠ACB=α,BG=x,EG=y. ①当α=900时,探索EG与BD的大小关系?并说明理由;
②当α=1200时,求y与x的关系式,并用x的代数式表示y.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读以下材料:
对数的创始人是苏格兰数学家纳皮尔(J.Nplcr,1550﹣1617年),纳皮尔发明对数是在指数书写方式之前,直到18世纪瑞士数学家欧拉(Evlcr,1707﹣1783年)才发现指数与对数之间的联系.
对数的定义:一般地,若ax=N(a>0,a≠1),那么x叫做以a为底N的对数,记作:x=logaN.比如指数式24=16可以转化为4=log216,对数式2=log525可以转化为52=25.
我们根据对数的定义可得到对数的一个性质:loga(MN)=logaM+logaN(a>0,a≠1,M>0,N>0);理由如下:
设logaM=m,logaN=n,则M=am,N=an
∴MN=aman=am+n,由对数的定义得m+n=loga(MN)
又∵m+n=logaM+logaN
∴loga(MN)=logaM+logaN
解决以下问题:
(1)将指数43=64转化为对数式_____;
(2)证明loga![]() =logaM﹣logaN(a>0,a≠1,M>0,N>0)
=logaM﹣logaN(a>0,a≠1,M>0,N>0)
(3)拓展运用:计算log32+log36﹣log34=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,三角形BCO是三角形BAO经过某种变换得到的.
(1)写出A,C的坐标;
(2)图中A与C的坐标之间的关系是什么?
(3)如果三角形AOB中任意一点M的坐标为(x,y),那么它的对应点N的坐标是什么?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com