

ЗжЮі ЃЈ1ЃЉЯШИљОнЙДЙЩЖЈРэЕУЃКa2+b2=c2ЃЌдйМЦЫуЙигкxЕФЗНГЬЃЈb+cЃЉx2+2ax+c-b=0жаЁїЕФжЕЃЌЛЏМђКѓНЋa2+b2=c2ДњШыЕУЃКЁї=0ЃЌЕУГіНсТлЃЛ
ЃЈ2ЃЉзїИЈжњЯпЃЌЙЙНЈШЋЕШШ§НЧаЮЃЌжЄУїЁїBDAЁеЁїBECЃЌЕУBA=BCЃЌЫЕУїЗНГЬx2-2px+q2=0гаСНИіЯрЕШЪЕИљЃЌдђЁї=0ЃЌДњШыМЦЫуПЩЕУpгыqЕФЙиЯЕЪНЃЛ
ЃЈ3ЃЉзїИЈжњЯпЃЌЙЙНЈжБНЧЁїFGCЃЌжЄУїЁїEAOЁеЁїFCOЃЌЕУЁїEOFЪЧЕШбќжБНЧШ§НЧаЮЃЌдйжЄУїЁїEAOЁзЁїFGPЃЌЕУ$\frac{EA}{FG}=\frac{AO}{PG}$ЃЌЫљвдAO=$\sqrt{2}$PGЃЌЫљвдPG=CQЃЌдђCG=PQ=1ЃЌДгЖјЧѓГіCFЕФГЄЃЎ
НтД№ жЄУїЃКЃЈ1ЃЉгЩЭМ1ПЩжЊЃКЁЯAOC=90ЁуЃЌ
ЁпOA=aЃЌOC=bЃЌAC=cЃЌ
Ёрa2+b2=c2ЃЌ
Ёрa2+b2-c2=0ЃЌ
ЙигкxЕФЗНГЬЃЈb+cЃЉx2+2ax+c-b=0ЃЌ
Ёї=ЃЈ2aЃЉ2-4ЃЈb+cЃЉЃЈc-bЃЉ=4a2+4b2-4c2ЃЌ
ЁрЁї=4ЃЈa2+b2-c2ЃЉ=0ЃЌ
ЁрЙигкxЕФЗНГЬЃЈb+cЃЉx2+2ax+c-b=0гаСНИіЯрЕШЕФЪЕЪ§ИљЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌp2=q2ЃЌРэгЩЪЧЃК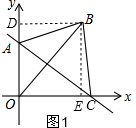
Й§BзїBDЁЭyжсЃЌBEЁЭxжсЃЌДЙзуЗжБ№ЮЊDЁЂEЃЌ
ЁрЁЯBDO=ЁЯBEO=90ЁуЃЌ
ЁпЁЯAOC=90ЁуЃЌ
ЁрЫФБпаЮDOEBЪЧОиаЮЃЌ
ЁрЁЯDBE=90ЁуЃЌ
ЁрЁЯDBA+ЁЯABE=90ЁуЃЌ
ЁпЁЯABC=90ЁуЃЌ
ЁрЁЯCBE+ЁЯABE=90ЁуЃЌ
ЁрЁЯDBA=ЁЯCBEЃЌ
ЁпOBЦНЗжЁЯAOCЃЌ
ЁрBD=BEЃЌ
ЁпЁЯBDO=ЁЯBEC=90ЁуЃЌ
ЁрЁїBDAЁеЁїBECЃЌ
ЁрBA=BCЃЌ
ЁпBAЃЌBCЮЊЗНГЬx2-2px+q2=0ЕФСНИљЃЌ
ЁрЁї=ЃЈ-2pЃЉ2-4ЁС1ЁСq2=0ЃЌ
p2-q2=0ЃЌ
Ёрp2=q2ЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌ Й§FзїFGЁЭACгкGЃЌ
Й§FзїFGЁЭACгкGЃЌ
ЁпOA=OCЃЌЁЯAOC=90ЁуЃЌ
ЁрЁїAOCЪЧЕШбќжБНЧШ§НЧаЮЃЌ
гЩЃЈ2ЃЉЕУЃКЁїABCвВЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЁрЫФБпаЮAOCBЮЊе§ЗНаЮЃЌ
ЁрЁЯACB=45ЁуЃЌ
ЁрЁїFGCЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЩшFG=CG=xЃЌдђFC=$\sqrt{2}$xЃЌAE=$\sqrt{2}$xЃЌ
ЁпAE=FCЃЌЁЯEAO=ЁЯOCF=90ЁуЃЌ
ЁрЁїEAOЁеЁїFCOЃЌ
ЁрEO=FOЃЌЁЯOEA=ЁЯOFCЃЌЁЯEOA=ЁЯFOCЃЌ
ЁпЁЯAOC=90ЁуЃЌ
ЁрЁЯAOF+ЁЯFOC=90ЁуЃЌ
ЁрЁЯEOA+ЁЯAOF=90ЁуЃЌ
ЁрЁЯEOF=90ЁуЃЌ
ЁрЁїEOFЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЁрЁЯOEF=45ЁуЃЌ
ЁпЁЯOFC=45Ёу+ЁЯGFOЃЌ
ЁЯOEA=45Ёу+ЁЯHEAЃЌ
ЁрЁЯGFO=ЁЯHEAЃЌ
ЁпЁЯEAH=ЁЯMGF=90ЁуЃЌ
ЁрЁЯEHA=ЁЯFMGЃЌ
ЁпЁЯEHA=ЁЯAOE+ЁЯOEF=ЁЯAOE+45ЁуЃЌ
ЁЯFMG=ЁЯOFE+ЁЯFPG=ЁЯFPG+45ЁуЃЌ
ЁрЁЯAOE=ЁЯFPGЃЌ
ЁпЁЯEAO=ЁЯFGP=90ЁуЃЌ
ЁрЁїEAOЁзЁїFGPЃЌ
Ёр$\frac{EA}{FG}=\frac{AO}{PG}$ЃЌ
Ёр$\frac{\sqrt{2}x}{x}=\frac{AO}{PG}$=$\sqrt{2}$ЃЌ
ЁрAO=$\sqrt{2}$PGЃЌ
ЁпЁїAOQЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЁрAO=$\sqrt{2}$OQЃЌ
ЁпOQ=CQЃЌ
ЁрAO=$\sqrt{2}$CQЃЌ
ЁрCQ=PGЃЌ
ЁрPQ=CGЃЌ
ЁпPQ=1ЃЌ
ЁрCG=1ЃЌ
Ёрx=1ЃЌ
ЁрCF=$\sqrt{2}$x=$\sqrt{2}$ЃЎ
ЕуЦР БОЬтЪЧШ§НЧаЮЕФзлКЯЬтЃЌПМВщСЫЕШбќжБНЧШ§НЧаЮЁЂОиаЮЁЂе§ЗНаЮЕФаджЪКЭХаЖЈЃЌгывЛдЊЖўДЮЗНГЬИљЕФЧщПіЯрНсКЯЃЌЪьСЗеЦЮеЁїгыЗНГЬИљЕФЧщПіЃКЂйЕБЁїЃО0ЪБЃЌЗНГЬгаСНИіВЛЯрЕШЕФСНИіЪЕЪ§ИљЃЛЂкЕБЁї=0ЪБЃЌЗНГЬгаСНИіЯрЕШЕФСНИіЪЕЪ§ИљЃЛЂлЕБЁїЃМ0ЪБЃЌЗНГЬЮоЪЕЪ§ИљЃЛЗДЙ§РДвВГЩСЂЃЛЭЌЪБРћгУЕШбќжБНЧШ§НЧаЮаББпгыжБНЧБп$\sqrt{2}$БЖЕФЙиЯЕЃЌЕУГіЯрЫЦШ§НЧаЮЖдгІБпЕФБШЃЌДгЖјХаЖЯГіЯпЖЮPG=CQЃЌЪЙЮЪЬтЕУвдНтОіЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | y=2x+3 | BЃЎ | y=-$\frac{3}{x}$ | CЃЎ | y=$\frac{2}{x}$ | DЃЎ | y=$\frac{3}{x}$ЃЈxЃО0ЃЉ |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com