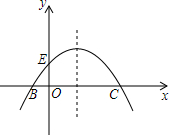Question

12．如图，已知抛物线y=-$\frac{1}{m}$（x+2）（x-m）（m＞0）与x轴相交于点B、C，与y轴相交于点E，且点B在点C的左侧．
（1）若抛物线过点M（2，2），求抛物线的解析式．
（2）在（1）的条件下，在抛物线的对称轴上找一点H，使BH+EH最小，并求出点H的坐标．

Answer 1

分析 （1）将点M的坐标代入抛物线的解析式得到关于m的方程，从而可求得m的值，故此可求得抛物线的解析式；
（2）将x=0代入得y=2，故此可知点E的坐标（0，2），然后由x=-$\frac{b}{2a}$，可知：x=1，点E关于x=1的对称点E′的坐标为（2，2）．令y=0得；$-\frac{1}{4}{x}^{2}+\frac{1}{2}x+2$=0，求得点B的坐标为（-2，0）．连接BE′交x=1于点H，点H即为所求作的点，然后依据待定系数法可求得直线BE′的解析式为y=$\frac{1}{2}x+1$．将x=1代入得：y=$\frac{3}{2}$，则点H的坐标为（1，$\frac{3}{2}$）．

解答 解：（1）将x=2，y=2代入函数的解析式得；-$\frac{1}{m}$（2+2）（2-m）=2．
解得：m=4．
∴抛物线的解析式为y=$-\frac{1}{4}{x}^{2}+\frac{1}{2}x+2$．
（2）如图所示；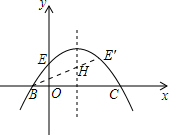

∵当x=0时，y=2，
∴点E的坐标是（0，2）．
∵x=-$\frac{b}{2a}$，
∴x=-$\frac{\frac{1}{2}}{-\frac{1}{4}×2}$=1．
点E关于x=1的对称点E′的坐标为（2，2）．
令y=0得；$-\frac{1}{4}{x}^{2}+\frac{1}{2}x+2$=0，
解得：x₁=-2，x₂=4．
∴点B的坐标为（-2，0）．
连接BE′交x=1于点H，点H即为所求作的点．
设直线BE′的解析式为y=kx+b．
将点B、E′的坐标代入得：$\left\{\begin{array}{l}{2k+b=2}\\{-2k+b=0}\end{array}\right.$，
解得b=1，k=$\frac{1}{2}$．
∴直线BE′的解析式为y=$\frac{1}{2}x+1$．
将x=1代入得：y=$\frac{3}{2}$．
∴点H的坐标为（1，$\frac{3}{2}$）．

点评 本题主要考查的是抛物线与坐标的交点、轴对称路径最短问题、求得点B、E′的坐标是解题的关键．