
【题目】注意:为了使同学们更好地解答本题的第(Ⅱ)问,我们提供了一种分析问题的方法,你可以依照这个方法按要求完成本题的解答,也可以选用其他方法,按照解答题的一般要求进行解答即可.
如图,将一个矩形纸片ABCD,放置在平面直角坐标系中,A(0,0),B(4,0),D(0,3),M是边CD上一点,将△ADM沿直线AM折叠,得到△ANM.
(Ⅰ)当AN平分∠MAB时,求∠DAM的度数和点M的坐标;
(Ⅱ)连接BN,当DM=1时,求△ABN的面积;
(Ⅲ)当射线BN交线段CD于点F时,求DF的最大值.(直接写出答案)
在研究第(Ⅱ)问时,师生有如下对话:
师:我们可以尝试通过加辅助线,构造出直角三角形,寻找方程的思路来解决问题.
小明:我是这样想的,延长MN与x轴交于P点,于是出现了Rt△NAP,…
小雨:我和你想的不一样,我过点N作y轴的平行线,出现了两个Rt△NAP,…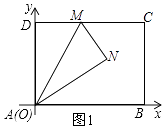
【答案】解:(Ⅰ)∵A(0,0),B(4,0),D(0,3),
∴AD=3,AB=4,
由折叠得:△ANM≌△ADM,
∴∠MAN=∠DAM,
∵AN平分∠MAB,
∴∠MAN=∠NAB,
∴∠BAM=∠MAN=∠NAB,
∵四边形ABCD是矩形,
∴∠DAB=90°,
∴∠DAM=30°,
∴DM=ADtan∠DAM=3×tan30°=3× ![]() =
= ![]() ,
,
∴∠DAM=30°,M( ![]() ,3);
,3);
(Ⅱ)延长MN交AB的延长线于点Q,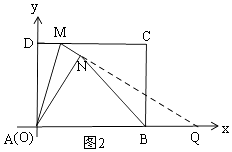
∵四边形ABCD是矩形,
∴AB∥CD,
∴∠DMA=∠MAQ,
由折叠得:△ANM≌△ADM,
∴∠DMA=∠AMQ,AN=AD=3,MN=MD=1,
∴∠MAQ=∠AMQ,
∴MQ=AQ,
设NQ=x,则AQ=MQ=1+x,
∵∠ANM=90°,
∴∠ANQ=90°,
在Rt△ANQ中,由勾股定理得:AQ2=AN2+NQ2 ,
∴(x+1)2=32+x2 ,
解得:x=4,
∴NQ=4,AQ=5,
∵AB=4,AQ=5,
∴S△NAB= ![]() =
= ![]() ×
× ![]() ANNQ=
ANNQ= ![]() ×3×4=
×3×4= ![]() ;
;
(Ⅲ)如图3,过A作AH⊥BF于H,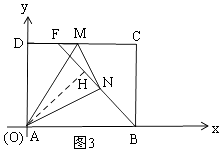
∵四边形ABCD是矩形,
∴AB∥CD,
∴∠AHB=∠BCF=90°,
∴△ABH∽△BFC,
∴ ![]() ,
,
Rt△AHN中,∵AH≤AN=3,AB=4,
∴当点N、H重合(即AH=AN)时,AH最大,BH最小,CF最小,DF最大,此时点M、F重合,B、N、M三点共线,如图4所示,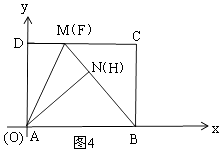
由折叠得:AD=AH,
∵AD=BC,
∴AH=BC,
在△ABH和△BFC中,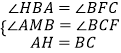 ,
,
∴△ABH≌△BFC(AAS),
∴CF=BH,
由勾股定理得:BH= ![]() =
= ![]() =
= ![]() ,
,
∴CF= ![]() ,
,
∴DF的最大值为DC﹣CF=4﹣ ![]()
【解析】(Ⅰ)由折叠的性质得:△ANM≌△ADM,由角平分线结合得:∠BAM=∠MAN=∠NAB=30°,由特殊角的三角函数可求DM的长,写出M的坐标;(Ⅱ)如图2,作辅助线,构建直角三角形,设NQ=x,则AQ=MQ=1+x,在Rt△ANQ中,由勾股定理列等式可得关于x的方程:(x+1)2=32+x2 , 求出x,得出AB是AQ的 ![]() ,即可得出△NAQ和△NAB的关系,得出结论;(Ⅲ)如图3,过A作AH⊥BF于H,证明△ABH∽△BFC,得
,即可得出△NAQ和△NAB的关系,得出结论;(Ⅲ)如图3,过A作AH⊥BF于H,证明△ABH∽△BFC,得 ![]() ,Rt△AHN中,∵AH≤AN=3,AB=4,可知:当点N、H重合(即AH=AN)时,AH最大,BH最小,CF最小,DF最大,此时点M、F重合,B、N、M三点共线,如图4所示,求此时DF的长即可.
,Rt△AHN中,∵AH≤AN=3,AB=4,可知:当点N、H重合(即AH=AN)时,AH最大,BH最小,CF最小,DF最大,此时点M、F重合,B、N、M三点共线,如图4所示,求此时DF的长即可.
【考点精析】利用勾股定理的概念和翻折变换(折叠问题)对题目进行判断即可得到答案,需要熟知直角三角形两直角边a、b的平方和等斜边c的平方,即;a2+b2=c2;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:
【题目】如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.
(1)请你数一数,图中有多少个小于平角的角;
(2)求出∠BOD的度数;
(3)请通过计算说明OE是否平分∠BOC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.
(1)求每台A型电脑和B型电脑的销售利润;
(2)该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
①求y关于x的函数关系式;
②该商店购进A型、B型电脑各多少台,才能使销售总利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为a(a>2)的正方形各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,则正方形MNPQ的面积为 . 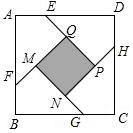
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某社区准备在甲乙两位射箭爱好者中选出一人参加集训,两人各射了5箭,他们的总成绩(单位:环)相同.
第1次 | 第2次 | 第3次 | 第4次 | 第5次 | |
甲成绩 | 9 | 4 | 7 | 4 | 6 |
乙成绩 | 7 | 5 | 7 | a | 7 |
(1)a=__,![]() =____;
=____;
(2)①分别计算甲、乙成绩的方差.
②请你从平均数和方差的角度分析,谁将被选中.
查看答案和解析>>
科目:初中数学 来源: 题型:
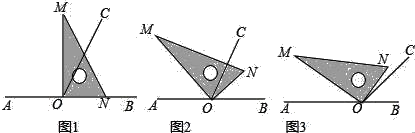
【题目】点O为直线AB上一点,过点O作射线OC,使∠BOC=65°.将一直角三角板的直角顶点放在点O处.
(1)如图①,将三角板MON的一边ON与射线OB重合时,则∠MOC= ;
(2)如图②,将三角板MON绕点O逆时针旋转一定角度,此时OC是∠MOB的角平分线,求旋转角∠BON= ;∠CON= .
(3)将三角板MON绕点O逆时针旋转至图③时,∠NOC=5°,求∠AOM.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课间休息时小明拿着两根木棒玩,小华看到后要小明给他玩,小明说:“较短木棒AB长40cm,较长木棒CD长60cm,将它们的一端重合,放在同一条直线上,此时两根木棒的中点分别是点E和点F,则点E和点F间的距离是多少?你说对了我就给你玩”聪明的你请帮小华求出此时两根木棒的中点E和F间的距离是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我们学习过的数学教科书中,有一个数学活动,其具体操作过程是:
第一步:对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展开(如图①);
第二步:再一次折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM,同时得到线段BN(如图②).
如图②所示建立平面直角坐标系,请解答以下问题:
(Ⅰ)设直线BM的解析式为y=kx,求k的值;
(Ⅱ)若MN的延长线与矩形ABCD的边BC交于点P,设矩形的边AB=a,BC=b;
(i)若a=2,b=4,求P点的坐标;
(ii)请直接写出a、b应该满足的条件.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图A在数轴上所对应的数为﹣2.
(1)点B在点A右边距A点4个单位长度,求点B所对应的数;
(2)在(1)的条件下,点A以每秒2个单位长度沿数轴向左运动,点 B 以每秒2个单位长度沿数轴向右运动,当点A运动到﹣6所在的点处时,求A,B两点间距离.
(3)在(2)的条件下,现A点静止不动,B点再以每秒2个单位长度沿数轴向左运动时,经过多长时间A,B两点相距4个单位长度.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com