
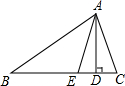
 如图,在△ABC中,AD⊥BC于D,AE为∠BAC的平分线,且∠DAE=15°,∠B=35°,则∠C=65°.
如图,在△ABC中,AD⊥BC于D,AE为∠BAC的平分线,且∠DAE=15°,∠B=35°,则∠C=65°.  学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
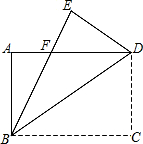 如图,有一个直角三角形纸片,两直角边AB=6cm,BC=8cm,现将直角边BC沿直线BD折叠,使点C落在点E处,求三角形BDF的面积是多少?
如图,有一个直角三角形纸片,两直角边AB=6cm,BC=8cm,现将直角边BC沿直线BD折叠,使点C落在点E处,求三角形BDF的面积是多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
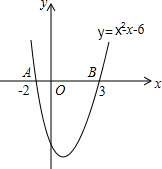 观察二次函数y=x2-x-6的图象,回答问题:
观察二次函数y=x2-x-6的图象,回答问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
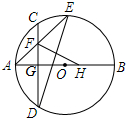 如图,AB是⊙O的直径,点A为$\widehat{CD}$的中点,点F是CG的中点,AF的延长线交⊙O于点E,点H是BG的中点,tanE=$\frac{1}{2}$.
如图,AB是⊙O的直径,点A为$\widehat{CD}$的中点,点F是CG的中点,AF的延长线交⊙O于点E,点H是BG的中点,tanE=$\frac{1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com