
【题目】在﹣9,﹣6,﹣3,﹣1,2,3,6,8,11这九个数中,任取一个作为a值,能够使关于x的一元二次方程x2+ax+9=0有两个不相等的实数根的概率是_____.
科目:初中数学 来源: 题型:
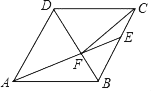
【题目】如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC,BD于点E,F,CE=2,连接CF.给出以下结论:①△ABF≌△CBF;②点E到AB的距离是3![]() ;③tan∠DCF=
;③tan∠DCF=![]() ;④△ABF的面积为
;④△ABF的面积为![]() .其中正确的结论序号是_____
.其中正确的结论序号是_____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)阅读理解
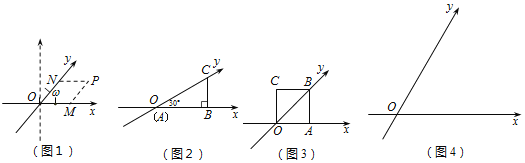
我们知道,平面内互相垂直且有公共原点的两条数轴构成平面直角坐标系.如果两条数轴不垂直,而是相交成任意的角ω(0°<ω<180°且ω≠90°),那么这两条数轴构成的是平面斜坐标系.如图1,经过平面内一点P作坐标轴的平行线PM和PN交x轴和y轴于M、N,点M、N在x轴和y轴上所对应的数分别叫做P点的x坐标和y坐标.
如图2,ω=30°,直角三角形的顶点A在坐标原点O,点B、C分别在x轴和y轴上,AB=![]() ,则点B、C在此斜坐标系内的坐标分别为B ,C .
,则点B、C在此斜坐标系内的坐标分别为B ,C .
(2)尝试应用
如图3,ω=45°,O为坐标原点,边长为1的正方形OABC一边OA在x轴上,设点G(x,y)在经过A、C两点的直线上,求y与x之间满足的关系式.
(3)深入探究
如图4,ω=60°,O为坐标原点,M(2,2),圆M的半径为![]() .有一个内角为60°的菱形,菱形的一边在x轴上,另有两边所在直线恰好与圆M相切,求此菱形的边长.
.有一个内角为60°的菱形,菱形的一边在x轴上,另有两边所在直线恰好与圆M相切,求此菱形的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象的对称轴是直线x=1,其图象的一部分如图所示.下列说法错误的是
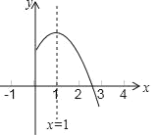
A. abc<0B. a﹣b+c<0C. 3a+c<0D. 当﹣1<x<3时,y>0
查看答案和解析>>
科目:初中数学 来源: 题型:
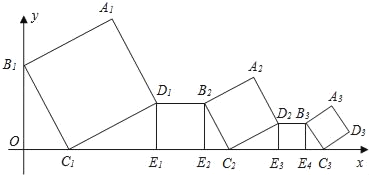
【题目】在平面直角坐标系中,正方形A1B1C1D1,D1E1E2B2,A2D2C2D2,D2E3E4B3,A3B3C3D3,…,按如图所示的方式放置,其中点B1在y轴上,点C1,E1,E2,C2,E3,E4,C3,…,在x轴上已知正方形A1,B1,C1,D1,的边长为1,∠OB1C1=30°,B1C1∥B2C2∥B3C3,…,则正方形AnBnnDn的边长是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在正方形ABCD中,点P沿边DA从点D开始向点A以1cm/s的速度移动:同时点Q沿边AB,BC从点A开始向点C以acm/s的速度移动,当点P移动到点A时,P,Q同时停止移动.设点P出发x秒时,△PAQ的面积为ycm2,y与x的函数图象如图②,线段EF所在的直线对应的函数关系式为y=﹣4x+21,则a的值为( )
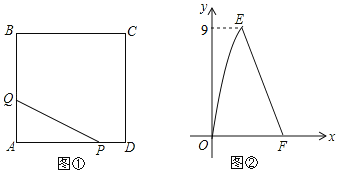
A. 1.5B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
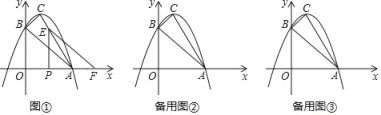
【题目】如图,已知抛物线y=﹣x2+bx+c与x轴的一个交点为A(3,0).与y轴的交点为B(0,3),其顶点为C.
(1)求抛物线的解析式;
(2)将△AOB沿x轴向右平移m个长度单位(0<m<3)后得到另一个△FPE,点A、O、B的像分别为点F、P、E.
①如图①,当点E在直线AC上时,求m的值.
②设所得的三角形△FPE与△ABC重叠部分的面积为S,求S关于m的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
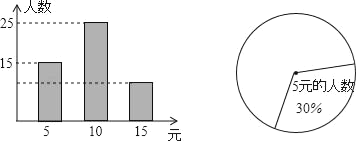
【题目】如图是某校九年级学生为灾区捐款情况抽样调查的条形图和扇形统计图.
(1)求抽样调查的人数;
(2)在扇形统计图中,求该样本中捐款15元的人数所占的圆心角度数;
(3)若该校九年级学生有1000人,据此样本估计九年级捐款总数为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com