
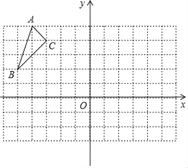
【题目】如图,△ABC的顶点坐标分别为A(﹣4,5),B(﹣5,2),C(﹣3,4)
(1)画出与△ABC关于原点O对称的△A1B1C1,并写出点A1的坐标为 ;
(2)D是x轴上一点,使DB+DC的值最小,画出点D(保留画图痕迹);
(3)P(t,0)是x轴上的动点,将点C绕点P顺时针旋转90°至点E,直线y=﹣2x+5经过点E,则t的值为 .
【答案】(1)(4,﹣5);(2)见解析;(3)﹣2.
【解析】
(1)利用关于原点对称点的坐标性质得出对应点位置进而得出答案.
(2)两点之间直线最短,作点B关于x轴的对称点B′,连接CB′交x轴得点.
(3)作CH⊥x轴于H,EK⊥x轴于K.证明△PCH≌△EPK,所以PK=CH=4,EK=PH=t+3,OK=4+t,得点E在直线y=﹣2x+5上,再代入直线y=﹣2x+5即可求解.
解:(1)△A1B1C1如图所示,A1(4,﹣5);
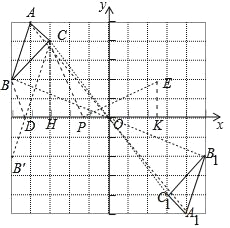
故答案为(4,﹣5).
(2)作点B关于x轴的对称点B′,连接CB′交x轴于点D,此时BD+CD的值最小;
(3)作CH⊥x轴于H,EK⊥x轴于K.
∵∠CHP=∠CPE=∠PKE=90°,
∴∠CPH+∠HCP=90°,∠CPH+∠EPK=90°,
∴∠PCH=∠EPK,∵PC=PE,
∴△PCH≌△EPK(AAS),
∴PK=CH=4,EK=PH=t+3,
∴OK=4+t,
∴E(4+t,t+3),
∵点E在直线y=﹣2x+5上,
∴t+3=﹣2(4+t)+5,
t=﹣2,
故答案为﹣2.


科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数y1=![]() 与一次函数y2=k2x+b的图象交于点A(1,8),B(-4,m)两点.
与一次函数y2=k2x+b的图象交于点A(1,8),B(-4,m)两点.
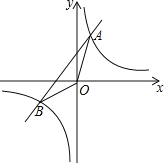
(1)求k1,k2,b的值;
(2)求△AOB的面积;
(3)请直接写出不等式![]() x+b的解.
x+b的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线l1∥l2∥l3,且l1与l2的距离为1.l2与l3的距离为2,把∠ACB=30°的直角三角板如图放置,顶点A,B,C恰好落在三条直线上,则线段AB的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形 ABCD 中,AE=AB,直线 DE 交 BC 于点 F,则∠BED 的度数是( )
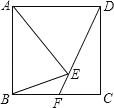
A. 105° B. 120° C. 135° D. 150°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场按定价销售某种电器时,每台可获利 48 元,按定价的九折销售该电器 6 台与将定价降低 30 元销售该电器 9 台所获得的利润相等,
(1)该电器每台进价、定价各是多少元?
(2)按(1)的定价该商场一年可销售这种电器 1000 台.经市场调查:每降低一元一年可多卖该种电器出 10 台.如果商场想在一年中使该种电器获利32670 元,那么商场应按几折销售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划在总费用2300元的限额内,租用客车送234名学生和6名教师集体外出活动,每辆客车上至少要有1名教师.现有甲、乙两种大客车,它们的载客量和租金如下表所示.
甲种客车 | 乙种客车 | |
载客量/(人/辆) | 45 | 30 |
租金/(元/辆) | 400 | 280 |
(1)共需租多少辆客车?
(2)请给出最节省费用的租车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着柴静纪录片《穹顶之下》的播出,全社会对空气污染问题越来越重视,空气净化器的销量也大增,商社电器从厂家购进了A,B两种型号的空气净化器,已知一台A型空气净化器的进价比一台B型空气净化器的进价多300元,用7500元购进A型空气净化器和用6000元购进B型空气净化器的台数相同.
(1)求一台A型空气净化器和一台B型空气净化器的进价各为多少元?
(2)在销售过程中,A型空气净化器因为净化能力强,噪音小而更受消费者的欢迎.为了增大B型空气净化器的销量,商社电器决定对B型空气净化器进行降价销售,经市场调查,当B型空气净化器的售价为1800元时,每天可卖出4台,在此基础上,售价每降低50元,每天将多售出1台,如果每天商社电器销售B型空气净化器的利润为3200元,请问商社电器应将B型空气净化器的售价定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】感知:如图①,在等腰直角△ABC中,分别以△ABC的三条边为斜边向△ABC外部作等腰直角△ABD、等腰直角△ACE、等腰直角△BCF,连结点D、E、F,则易知△DEF为等腰三角形.如果AB=AC=7,请直接写出△DEF的面积为 .
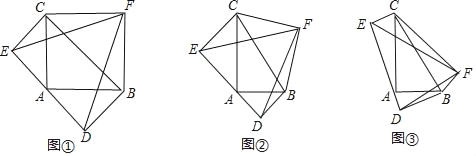
探究:如图②,Rt△ABC中,AB=14,AC=30,分别以△ABC的三条边为斜边向△ABC外部作等腰直角△ABD、等腰直角△ACE、等腰直角△BCF,连结点D、E、F,求△DEF的面积为多少.
拓展:如图③,Rt△ABC中,AB=14,AC=15,分别以△ABC的三条边为斜边向△ABC外部作Rt△ABD、Rt△ACE、Rt△BCF,且tan∠BCF=tan∠CAE=tan∠ABD=![]() ,连结点D、E、F,则△DEF的面积为 .
,连结点D、E、F,则△DEF的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对称轴为直线x=1的抛物线y=ax2+bx+8过点(﹣2,0).
(1)求抛物线的表达式,并写出其顶点坐标;
(2)现将此抛物线沿y轴方向平移若干个单位,所得抛物线的顶点为D,与y轴的交点为B,与x轴负半轴交于点A,过B作x轴的平行线交所得抛物线于点C,若AC∥BD,试求平移后所得抛物线的表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com