
【题目】感知:如图①,在等腰直角△ABC中,分别以△ABC的三条边为斜边向△ABC外部作等腰直角△ABD、等腰直角△ACE、等腰直角△BCF,连结点D、E、F,则易知△DEF为等腰三角形.如果AB=AC=7,请直接写出△DEF的面积为 .
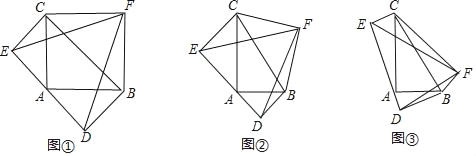
探究:如图②,Rt△ABC中,AB=14,AC=30,分别以△ABC的三条边为斜边向△ABC外部作等腰直角△ABD、等腰直角△ACE、等腰直角△BCF,连结点D、E、F,求△DEF的面积为多少.
拓展:如图③,Rt△ABC中,AB=14,AC=15,分别以△ABC的三条边为斜边向△ABC外部作Rt△ABD、Rt△ACE、Rt△BCF,且tan∠BCF=tan∠CAE=tan∠ABD=![]() ,连结点D、E、F,则△DEF的面积为 .
,连结点D、E、F,则△DEF的面积为 .
【答案】感知: 49;探究: 484;拓展: 168.15.
【解析】
感知:只要证明E、A、D共线,FA⊥DE,想办法求出DE、AF即可;
探究:如图②中,连接AF.作FM⊥AB于M,FN⊥AC于N.解法类似;
拓展:如图③中,连接AF,作BH⊥AF于H.解法类似;
解:感知:如图①中,连接AF.
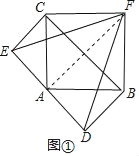
∵AC=AB,∠BAC=90°,△ACE,△ABD都是等腰直角三角形,
∴EC=AE=AD=BD,∠CAE=∠BAD=45°
∴∠CAE+∠CAB+∠BAD=180°,
∴E、A、D共线,
∵CF=FB,∠FCE=∠FBD,CE=BD,
∴△CFE≌△BFD,
∴FE=FD,∵AE=AD,
∴FA⊥DE,
∴![]()
探究:如图②中,连接AF.作FM⊥AB于M,FN⊥AC于N.
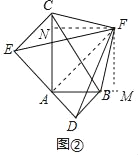
同理可证E、A、D共线,
∵∠BAC+∠CFB=180°,
∴A、B、F、C四点共圆,
∴∠FAB=∠FCB=45°,∵∠BAD=45°,
∴∠FAD=90°,
∴FA⊥DE,
∵∠FAC=∠FAB,FM⊥AB于M,FN⊥AC于N.
∴FN=FM,
∵FC=FB,
∴△FCN≌△FBM,
∴FN=FM=AM=AN,CN=BM,
∴AN+AM=AC﹣CN+AM﹣BM=44,
∴AM=FM=22,
∴![]()
∴![]()
(3)拓展:如图③中,连接AF,作BH⊥AF于H.
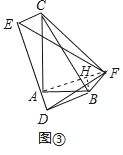
同法可证E、A、D共线,AF⊥DE,
易知: ![]()
由△FHB∽△CAB,可得: ![]()
∴![]()
∴![]()
∴![]()
故答案为49,484,168.15.


科目:初中数学 来源: 题型:
【题目】某测量队在山脚A处测得山上树顶仰角为45°(如图),测量队在山坡上前进600米到D处,再测得树顶的仰角为60°,已知这段山坡的坡角为30°,如果树高为15米,则山高为( )(精确到1米, ![]() =1.732).
=1.732).

A. 585米 B. 1014米 C. 805米 D. 820米
查看答案和解析>>
科目:初中数学 来源: 题型:
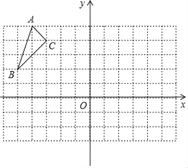
【题目】如图,△ABC的顶点坐标分别为A(﹣4,5),B(﹣5,2),C(﹣3,4)
(1)画出与△ABC关于原点O对称的△A1B1C1,并写出点A1的坐标为 ;
(2)D是x轴上一点,使DB+DC的值最小,画出点D(保留画图痕迹);
(3)P(t,0)是x轴上的动点,将点C绕点P顺时针旋转90°至点E,直线y=﹣2x+5经过点E,则t的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年3月国际风筝节期间,王大伯决定销售一批风筝,经市场调研:蝙蝠型风筝进价每个为10元,当售价每个为12元时,销售量为180个,若售价每提高1元,销售量就会减少10个,请回答以下问题:
(1)用表达式表示蝙蝠型风筝销售量y(个)与售价x(元)之间的函数关系(12≤x≤30);
(2)王大伯为了让利给顾客,并同时获得840元利润,售价应定为多少?
(3)当售价定为多少时,王大伯获得利润W最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE、AF、EF.

(1)求证:△ADE≌△ABF;
(2)填空:△ABF可以由△ADE绕旋转中心 点,按顺时针方向旋转 度得到;
(3)若BC=8,DE=6,求△AEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个箱子里放有1个白球和2个红球,它们除颜色外其余都相同.
(1)从箱子里摸出1个球,是黑球,这属于什么事件;(填“必然”、“不可能”或“随机”)
(2)从箱子里摸出1个球,放回,摇匀后再摸出一个球,请利用树状图或表格计算,这样先后摸得的两个球都是红球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点G,D,C在直线a上,点E,F,A,B在直线b上,若a∥b,Rt△GEF从如图所示的位置出发,沿直线b向右匀速运动,直到EG与BC重合.运动过程中△GEF与矩形ABCD重合部分的面积(S)随时间(t)变化的图象大致是( )

A.  B.
B.  C.
C. 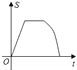 D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某隧道洞的内部截面顶部是抛物线形,现测得地面宽 AB=10m,隧道顶点O到地面AB的距离为5m,
(1)建立适当的平面直角坐标系,幵求该抛物线的解析式;
(2)一辆小轿车长 4.5米,宽2米,高1.5米,同样大小的小轿车通过该隧道,最多能有 几辆车幵行?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店从厂家以21元的价格购进一批商品,该商品可以自行定价,若每件商品售价为![]() 元,则可卖出(350-10
元,则可卖出(350-10![]() )件,但物价局限定每件商品加价不能超过进价的20%,商店计划要赚400元,需要卖出多少件商品?每件商品应售多少元?
)件,但物价局限定每件商品加价不能超过进价的20%,商店计划要赚400元,需要卖出多少件商品?每件商品应售多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com