
【题目】如图,点G,D,C在直线a上,点E,F,A,B在直线b上,若a∥b,Rt△GEF从如图所示的位置出发,沿直线b向右匀速运动,直到EG与BC重合.运动过程中△GEF与矩形ABCD重合部分的面积(S)随时间(t)变化的图象大致是( )

A.  B.
B.  C.
C. 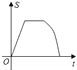 D.
D. 
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,等边△ABC的边长是2,D,E分别为AB,AC的中点,延长BC至点F,使CF=![]() BC连接CD和EF.
BC连接CD和EF.
(1)求证:DE=CF;
(2)求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A,B两点在数轴上,点A表示的数为-10,OB=3OA,点M以每秒3个单位长度的速度从点A向右运动.点N以每秒2个单位长度的速度从点O向右运动(点M、点N同时出发)
(1)数轴上点B对应的数是______.
(2)经过几秒,点M、点N分别到原点O的距离相等?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是按规律摆放在墙角的一些小正方体,从上往下分别记为第一层,第二层,第三层,…,第n层.
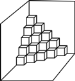
(1)第三层有________个小正方体;
(2)从第四层至第六层(含第四层和第六层)共有________个小正方体;
(3)第n层有________个小正方体;
(4)若每个小正方体边长为a分米,共摆放了n层,则要将摆放的小正方体能看到的表面部分涂上防锈漆,则防锈漆的总面积为________平方分米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:
3﹣![]() =3×
=3×![]() ;
;
(﹣![]() )﹣6=(﹣
)﹣6=(﹣![]() )×6;
)×6;
(﹣0.5)﹣(﹣1)=(﹣0.5)×(﹣1)
根据上面这些等式反映的规律,解答下列问题:
(1)上面等式反映的规律用文字语言可以描述如下:存在两个有理数,使得这两个有理数的差等于
.
(2)若满足上述规律的两个有理数中有一个数是![]() ,求另一个有理数;
,求另一个有理数;
(3)若这两个有理数用字母a、b表示,则上面等式反映的规律用字母表示为 ;
(4)在(3)中的关系式中,字母a、b是否需要满足一定的条件?若需要,直接写出字母a、b应满足的条件;若不需要,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A是双曲线y= ![]() (x>0)上一点,过点A作AB∥y轴,交双曲线y=﹣
(x>0)上一点,过点A作AB∥y轴,交双曲线y=﹣ ![]() (x>0)于点B,过点B作BC⊥AB交y轴于点C,连接AC,则△ABC的面积为 .
(x>0)于点B,过点B作BC⊥AB交y轴于点C,连接AC,则△ABC的面积为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
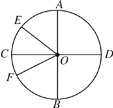
【题目】如图,圆O的直径为10 cm,两条直径AB,CD相交成90°角,∠AOE=50°,OF是∠BOE的平分线.
(1)求圆心角∠COF的度数;
(2)求扇形COF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一架方梯AB长25米,如图所示,斜靠在一面上:

(1)若梯子底端离墙7米,这个梯子的顶端距地面有多高?
(2)在(1)的条件下,如果梯子的顶端下滑了4米,那么梯子的底端在水平方向滑动了几米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=k1x﹣1的图象经过A(0,﹣1)、B(1,0)两点,与反比例函数y= ![]() 的图象在第一象限内的交点为M,若△OBM的面积为1.
的图象在第一象限内的交点为M,若△OBM的面积为1.
(1)求一次函数和反比例函数的表达式;
(2)在x轴上是否存在点P,使AM⊥PM?若存在,求出点P的坐标;若不存在,说明理由;
(3)x轴上是否存在点Q,使△QBM∽△OAM?若存在,求出点Q的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com