
【题目】如图,一次函数y=k1x﹣1的图象经过A(0,﹣1)、B(1,0)两点,与反比例函数y= ![]() 的图象在第一象限内的交点为M,若△OBM的面积为1.
的图象在第一象限内的交点为M,若△OBM的面积为1.
(1)求一次函数和反比例函数的表达式;
(2)在x轴上是否存在点P,使AM⊥PM?若存在,求出点P的坐标;若不存在,说明理由;
(3)x轴上是否存在点Q,使△QBM∽△OAM?若存在,求出点Q的坐标;若不存在,说明理由.
【答案】
(1)
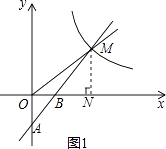
解:如图1,过点M作MN⊥x轴于点N,
∵一次函数y=k1x﹣1的图象经过A(0,﹣1)、B(1,0)两点,
∴0=k1﹣1,AO=BO=1,
解得:k1=1,
故一次函数解析式为:y=x﹣1,
∵△OBM的面积为1,BO=1,
∴M点纵坐标为:2,
∵∠OAB=∠MNB,∠OBA=∠NBM,
∴△AOB∽△MNB,
∴ ![]() =
= ![]() =
= ![]() ,
,
则BN=2,
故M(3,2),
则xy=k2=6,
故反比例函数解析式为:y= ![]()
(2)
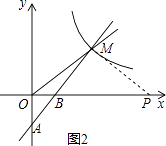
解:如图2,过点M作PM⊥AM,垂足为M,
∵∠AOB=∠PMB,∠OBA=∠MBP,
∴△AOB∽△PMB,
∴ ![]() =
= ![]() ,
,
由(1)得:AB= ![]() =
= ![]() ,BM=
,BM= ![]() =2
=2 ![]() ,
,
故 ![]() =
= ![]() ,
,
解得:BP=4,
故P(5,0)
(3)
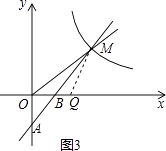
解:如图3,∵△QBM∽△OAM,
∴ ![]() =
= ![]() ,
,
由(2)可得AM=3 ![]() ,
,
故 ![]() =
= ![]() ,
,
解得:QB= ![]() ,
,
则OQ= ![]() ,
,
故Q点坐标为:( ![]() ,0).
,0).
【解析】(1)利用已知点B坐标代入一次函数解析式得出答案,再利用△OBM的面积得出M点纵坐标,再利用相似三角形的判定与性质得出M点坐标即可得出反比例函数解析式;(2)过点M作PM⊥AM,垂足为M,得出△AOB∽△PMB,进而得出BP的长即可得出答案;(3)利用△QBM∽△OAM,得出 ![]() =
= ![]() ,进而得出OQ的长,即可得出答案.
,进而得出OQ的长,即可得出答案.
【考点精析】通过灵活运用反比例函数的性质和相似三角形的性质,掌握性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大;对应角相等,对应边成比例的两个三角形叫做相似三角形即可以解答此题.


科目:初中数学 来源: 题型:
【题目】如图,点G,D,C在直线a上,点E,F,A,B在直线b上,若a∥b,Rt△GEF从如图所示的位置出发,沿直线b向右匀速运动,直到EG与BC重合.运动过程中△GEF与矩形ABCD重合部分的面积(S)随时间(t)变化的图象大致是( )

A.  B.
B.  C.
C. 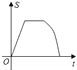 D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AD、BE、CF分别是三边上的中线.
(1)若AC=1,BC=![]() .求证:AD2+CF2=BE2;
.求证:AD2+CF2=BE2;
(2)是否存在这样的Rt△ABC,使得它三边上的中线AD、BE、CF的长恰好是一组勾股数?请说明理由.(提示:满足关系a2+b2=c2的3个正整数a、b、c称为勾股数.)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一个整数能表示成a2+b2(a、b是正整数)的形式,则称这个数为“丰利数”.例如,2是“丰利数”,因为2=12+12,再如,M=x2+2xy+2y2=(x+y)2+y2(x+y,y是正整数),所以M也是“丰利数”.
(1)请你写一个最小的三位“丰利数”是 ,并判断20 “丰利数”.(填是或不是);
(2)已知S=x2+y2+2x﹣6y+k(x、y是整数,k是常数),要使S为“丰利数”,试求出符合条件的一个k值(10≤k<200),并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD∥BC,AF平分∠BAD交BC于点F,BE平分∠ABC交AD于点E.求证: 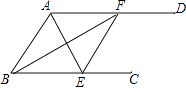
(1)△ABF是等腰三角形;
(2)四边形ABFE是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
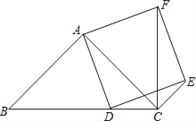
【题目】如图,已知在△ABC中,∠BAC=90°,AB=AC,点D在边BC上,以AD为边作正方形ADEF,连结CF,CE.
(1)求证:△ABD≌△ACF;
(2)如果BD=AC,求证:CD=CE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
学习了三角形全等的判定方法(即“SAS”“ASA”“AAS”“SSS”)和直角三角形全等的判定方法(即“HL”)后,小聪继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究
小聪将命题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E.
小聪的探究方法是对∠B分为“直角、钝角、锐角”三种情况进行探究.
第一种情况:当∠B 是直角时,如图1,△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E=90°,根据“HL”定理,可以知道Rt△ABC≌Rt△DEF.
第二种情况:当∠B 是锐角时,如图2,BC=EF,∠B=∠E<90°,在射线EM上有点D,使DF=AC,画出符合条件的点D,则△ABC和△DEF的关系是 ;
A.全等 B.不全等 C.不一定全等
第三种情况:当∠B是钝角时,如图3,在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E>90°.过点C作AB边的垂线交AB延长线于点M;同理过点F作DE边的垂线交DE延长线于N,根据“ASA”,可以知道△CBM≌△FEN,请补全图形,进而证出△ABC≌△DEF.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com