
【题目】解方程:
(1)![]() ;
;
(2)![]() ;
;
(3)![]() ;
;
(4)![]() .
.
【答案】(1)0.5;(2)无解;(3)无解;(4)![]()
【解析】试题分析:(1)、(2)、(3)、(4)都是方程两边同时乘以最简公分母,化为整式方程,解整式方程后进行检验即可得.
试题解析:(1)方程两边同时乘以2(x-1),得
2=3+2(x-1),
解得:x=0.5,
检验:当x=0.5时,2(x-1)≠0,
所以x=0.5是原方程的解;
(2)方程两边同时乘以x(x+1)(x-1),得
7(x-1)+3(x+1)=6x,
解得:x=1,
检验:当x=1时,x(x+1)(x-1)=0,所以原方程无解;
(3)方程两边同时乘以x(x-1),得
x2+x-2=x(x-1),
解得:x=1,
检验:当x=1时,x(x-1)=0,所以原方程无解;
(4)方程两边同时乘以2(x-2),得
3-2x=2(x-2),
解得:x=![]() ,
,
检验:当x=![]() 时,2(x-2)≠0,
时,2(x-2)≠0,
所以x=![]() 是原方程的解.
是原方程的解.


 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:
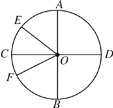
【题目】如图,圆O的直径为10 cm,两条直径AB,CD相交成90°角,∠AOE=50°,OF是∠BOE的平分线.
(1)求圆心角∠COF的度数;
(2)求扇形COF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富少年儿童的业余生活,某社区要在如图所示AB所在的直线建一图书室,本社区有两所学校所在的位置在点C和点D处,CA⊥AB于A,DB⊥AB于B,已知AB=25km,CA=15km,DB=10km,试问:图书室E应该建在距点A多少km处,才能使它到两所学校的距离相等?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=k1x﹣1的图象经过A(0,﹣1)、B(1,0)两点,与反比例函数y= ![]() 的图象在第一象限内的交点为M,若△OBM的面积为1.
的图象在第一象限内的交点为M,若△OBM的面积为1.
(1)求一次函数和反比例函数的表达式;
(2)在x轴上是否存在点P,使AM⊥PM?若存在,求出点P的坐标;若不存在,说明理由;
(3)x轴上是否存在点Q,使△QBM∽△OAM?若存在,求出点Q的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( ) 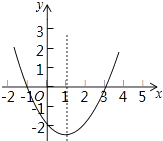
A.函数有最小值
B.当﹣1<x<3时,y>0
C.当x<1时,y随x的增大而减小
D.对称轴是直线x=1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是直线AB上任一点,射线OD和射线OE分别平分∠AOC和∠BOC.

(1)填空:与∠AOE互补的角是 ;
(2)若∠AOD=36°,求∠DOE的度数;
(3)当∠AOD=x°时,请直接写出∠DOE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读思考
我们知道,在数轴上|a|表示数a所对应的点到原点的距离,这是绝对值的几何意义,由此我们可进一步地来研究数轴上任意两个点之间的距离,一般地,如果数轴上两点A、B 对立的数用a,b表示,那么这两个点之间的距离AB=|a﹣b|.也可以用两点中右边的点所表示数的减去左边的点所表示的数来计算,例如:数轴上P,Q两点表示的数分别是﹣1和2,那么P,Q两点之间的距离就是 PQ=2﹣(﹣1)=3.
启发应用
如图,点A在数轴上对应的数为a,点B对应的数为b,且a、b满足|a+3|+(b﹣2)2=0
(1)求线段AB的长;
(2)如图,点C在数轴上对应的数为x,且x是方程2x+1=![]() x﹣8的解,
x﹣8的解,
①求线段BC的长;
②在数轴上是否存在点P使PA+PB=BC?若存在,直接写出点P对应的数:若不存在,说明理由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题.
 程大位,明代商人,珠算发明家,被称为珠算之父、卷尺之父.少年时,读书极为广博,对数学颇感兴趣,60岁时完成其杰作《直指算法统宗》(简称《算法统宗》).
程大位,明代商人,珠算发明家,被称为珠算之父、卷尺之父.少年时,读书极为广博,对数学颇感兴趣,60岁时完成其杰作《直指算法统宗》(简称《算法统宗》).
在《算法统宗》里记载了一道趣题:一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚各几丁?意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完.试问大、小和尚各多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAC=∠DAF=90°,AB=AC,AD=AF,点D、E为BC边上的两点,且∠DAE=45°,连接EF、BF,则下列结论:①△AED≌△AEF ②△AED为等腰三角形
③BE+DC>DE④BE2+DC2=DE2,其中正确的有( )个
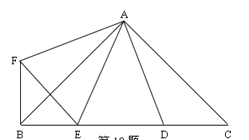
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com