
【题目】二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( ) 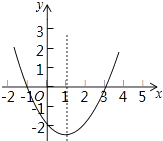
A.函数有最小值
B.当﹣1<x<3时,y>0
C.当x<1时,y随x的增大而减小
D.对称轴是直线x=1
科目:初中数学 来源: 题型:
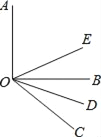
【题目】如图所示,OE,OD分别平分∠AOC和∠BOC,
(1)如果∠AOB=90°,∠BOC=38°,求∠DOE的度数;
(2)如果∠AOB=α,∠BOC=β(α、β均为锐角,α>β),其他条件不变,求∠DOE;
(3)从(1)、(2)的结果中,你发现了什么规律,请写出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司拟为贫困山区建一所希望小学,甲、乙两个工程队提交了投标方案,若独立完成该项目,则甲工程队所用时间是乙工程队的1.5倍;若甲、乙两队合作完成该项目,则共需72天.
(1)甲、乙两队单独完成建校工程各需多少天?
(2)若由甲工程队单独施工,平均每天的费用为0.8万元,为了缩短工期,该公司选择了乙工程队,但要求其施工的总费用不能超过甲工程队,求乙工程队平均每天的施工费用最多为多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD∥BC,AF平分∠BAD交BC于点F,BE平分∠ABC交AD于点E.求证: 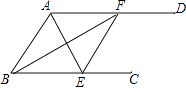
(1)△ABF是等腰三角形;
(2)四边形ABFE是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC是边长为4的等边三角形,BC在x轴上,点D为BC的中点,点A在第一象限内,AB与y轴的正半轴交与点E,已知点B(﹣1,0).
(1)点A的坐标: , 点E的坐标:;
(2)若二次函数y=﹣ ![]() x2+bx+c过点A、E,求此二次函数的解析式;
x2+bx+c过点A、E,求此二次函数的解析式;
(3)P是AC上的一个动点(P与点A、C不重合)连结PB、PD,设l是△PBD的周长,当l取最小值时,求点P的坐标及l的最小值并判断此时点P是否在(2)中所求的抛物线上,请充分说明你的判断理由.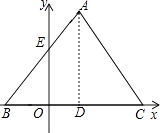
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为2 ![]() 的正方形ABCD中,点E为AD边的中点,将△ABE沿BE翻折,使点A落在点A′处,作射线EA′,交BC的延长线于点F,则CF= .
的正方形ABCD中,点E为AD边的中点,将△ABE沿BE翻折,使点A落在点A′处,作射线EA′,交BC的延长线于点F,则CF= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=ax2+bx+3(a≠0)与x轴、y轴分别交于点A(﹣1,0)、B(3,0)、点C三点.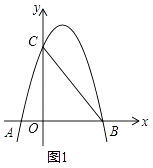
(1)试求抛物线的解析式;
(2)点D(2,m)在第一象限的抛物线上,连接BC,BD.试问,在对称轴左侧的抛物线上是否存在一点P,满足∠PBC=∠DBC?如果存在,请求出点P点的坐标;如果不存在,请说明理由;
(3)如图2,在(2)的条件下,将△BOC沿x轴正方向以每秒1个单位长度的速度向右平移,记平移后的三角形为△B′O′C′.在平移过程中,△B′O′C′与△BCD重叠的面积记为S,设平移的时间为t秒,试求S与t之间的函数关系式?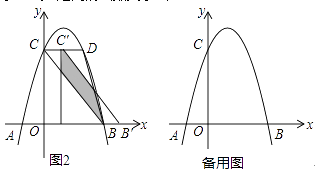
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】麒麟区第七中学现有一块空地ABCD如图所示,现计划在空地上种草皮,经测量,∠B=90°,AB=3m,BC=4m,CD=13m,AD=12m.

(1)求出空地ABCD的面积?
(2)若每种植1平方米草皮需要300元,问总共需投入多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com