
【题目】某商场按定价销售某种电器时,每台可获利 48 元,按定价的九折销售该电器 6 台与将定价降低 30 元销售该电器 9 台所获得的利润相等,
(1)该电器每台进价、定价各是多少元?
(2)按(1)的定价该商场一年可销售这种电器 1000 台.经市场调查:每降低一元一年可多卖该种电器出 10 台.如果商场想在一年中使该种电器获利32670 元,那么商场应按几折销售?
【答案】(1)该电器每台的进价是 162 元,定价是 210 元;(2)如果商场想在一年中使该种电器获利 32670 元,那么商场应按九折销售.
【解析】
(1)通过理解题意可知本题的两个等量关系,即定价﹣进价=48,6×(90%×定价﹣进价)=9×(定价﹣30﹣进价),根据这两个等量关系可列出方程组,求解即可;
(2)设商场降低 a 元销售,由商场想在一年中使该种电器获利 32670 元,得到方程(48﹣a)(1000+10a)=32670,解方程求出 a 的值,进而求解.
(1)设该电器每台的进价为 x 元,定价为 y 元,由题意得,
![]()
解得:![]()
答:该电器每台的进价是 162 元,定价是 210 元;
(2)设商场降低 a 元销售,由题意,得
(48﹣a)(1000+10a)=32670,
整理,得a2+52a﹣1533=0,
解得 a1=21,a2=﹣73(不合题意舍去).
![]() =0.9=9 折.
=0.9=9 折.
答:如果商场想在一年中使该种电器获利 32670 元,那么商场应按九折销售.


科目:初中数学 来源: 题型:
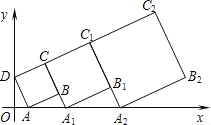
【题目】在平面直角坐标系中,第一个正方形ABCD的位置如图所示,点A的坐标为(2,0),点D的坐标为(0,4).延长CB交x轴于点A1,作第二个正方形A1B1C1C;延长C1B1交x轴于点A2,作第三个正方形A2B2C2C1,…,按这样的规律进行下去,第2016个正方形的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
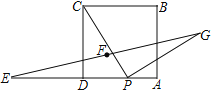
【题目】如图,正方形ABCD的边长为4,点E为AD的延长线上一点,且DE=DC,点P为边AD上一动点,且PC⊥PG,PG=PC,点F为EG的中点.当点P从D点运动到A点时,则CF的最小值为___________
查看答案和解析>>
科目:初中数学 来源: 题型:
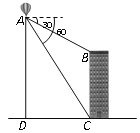
【题目】热气球的探测器显示,从热气球底部A处看一栋高楼顶部的俯角为30°,看这栋楼底部的俯角为60°,热气球A处与地面距离为420米,求这栋楼的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
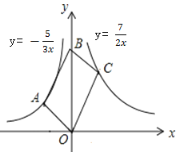
【题目】如图,平行四边形OABC的顶点O,B在y轴上,顶点A在反比例函数y=![]() 上,顶点C在反比例函数y=
上,顶点C在反比例函数y=![]() 上,则平行四边形OABC的面积是____________.
上,则平行四边形OABC的面积是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
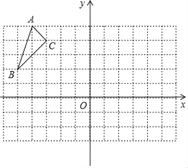
【题目】如图,△ABC的顶点坐标分别为A(﹣4,5),B(﹣5,2),C(﹣3,4)
(1)画出与△ABC关于原点O对称的△A1B1C1,并写出点A1的坐标为 ;
(2)D是x轴上一点,使DB+DC的值最小,画出点D(保留画图痕迹);
(3)P(t,0)是x轴上的动点,将点C绕点P顺时针旋转90°至点E,直线y=﹣2x+5经过点E,则t的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
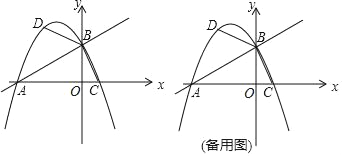
【题目】如图,直线y=![]() x+2与x轴交于点A,与y轴交于点B,抛物线y=﹣
x+2与x轴交于点A,与y轴交于点B,抛物线y=﹣![]() x2+bx+c经过A、B两点,与x轴的另一个交点为 C.
x2+bx+c经过A、B两点,与x轴的另一个交点为 C.
(1)求抛物线的解析式;
(2)直线AB上方抛物线上的点D,使得∠DBA=2∠BAC,求D点的坐标;
(3)M是平面内一点,将△BOC绕点M逆时针旋转90°后,得到△B1O1C1,若△B1O1C1的两个顶点恰好落在抛物线上,请求点B1的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE、AF、EF.

(1)求证:△ADE≌△ABF;
(2)填空:△ABF可以由△ADE绕旋转中心 点,按顺时针方向旋转 度得到;
(3)若BC=8,DE=6,求△AEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售一款进价为每件40元的护肤品,调查发现,销售单价不低于40元且不高于80元时,该商品的日销售量y(件)与销售单价x(元)之间存在一次函数关系,当销售单价为44元时,日销售量为72件;当销售单价为48元时,日销售量为64件.
(1)求y与x之间的函数关系式;
(2)设该护肤品的日销售利润为w(元),当销售单价x为多少时,日销售利润w最大,最大日销售利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com