
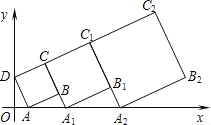
【题目】在平面直角坐标系中,第一个正方形ABCD的位置如图所示,点A的坐标为(2,0),点D的坐标为(0,4).延长CB交x轴于点A1,作第二个正方形A1B1C1C;延长C1B1交x轴于点A2,作第三个正方形A2B2C2C1,…,按这样的规律进行下去,第2016个正方形的面积为_____.
【答案】20×![]()
【解析】
先求出正方形ABCD的边长和面积,再求出第一个正方形A1B1C1C的面积,得出规律,根据规律即可求出第2016个正方形的面积.
解:∵点A的坐标为(2,0),点D的坐标为(0,4),
∴OA=2,OD=4
∵∠AOD=90°,
∴AB=AD=![]() ,∠ODA+∠OAD=90°,
,∠ODA+∠OAD=90°,
∵四边形ABCD是正方形,
∴∠BAD=∠ABC=90°,S正方形ABCD=(2![]() )2=20,
)2=20,
∴∠ABA1=90°,∠OAD+∠BAA1=90°,
∴∠ODA=∠BAA1,
∴△ABA1∽△DOA,
∴![]() =
=![]() ,即
,即![]() =
=![]()
∴BA1=![]() ,
,
∴CA1=![]() ,
,
∴正方形A1B1C1C的面积=(![]()
![]() )2=20×(
)2=20×(![]() )2…,第n个正方形的面积为20×(
)2…,第n个正方形的面积为20×(![]() )2n﹣2,
)2n﹣2,
∴第2016个正方形的面积20×(![]() )4030.
)4030.
故答案为:20×(![]() )4030.
)4030.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
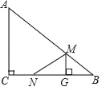
【题目】如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm.动点M从点B出发,在BA边上以每秒3cm的速度向定点A运动,同时动点N从点C出发,在CB边上以每秒2cm的速度向点B运动,且MG⊥BC,运动时间为t秒(0<t<![]() ),连接MN.
),连接MN.
(1)用含t的式子表示MG;
(2)当t为何值时,四边形ACNM的面积最小?并求出最小面积;
(3)若△BMN与△ABC相似,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在目前万物互联的时代,人工智能正掀起一场影响深刻的技术革命.谷歌、苹果、BAT、华为……巨头们纷纷布局人工智能。有人猜测,互联网过后,我们可能会迎来机器人。教育从幼儿抓起,近年来我国国内幼儿教育机器人发展趋势迅猛,市场上出现了满足各类要求的幼教机器人产品.“双十一”当天,某品牌幼教机器人专卖店抓住机遇,对最畅销的![]() 款幼教机器人进行促销,一台
款幼教机器人进行促销,一台![]() 款幼教机器人的成本价为850元,标价为1300元.
款幼教机器人的成本价为850元,标价为1300元.
(1)一台![]() 款幼教机器人的价格最多降价多少元,才能使利润率不低于30%;
款幼教机器人的价格最多降价多少元,才能使利润率不低于30%;
(2)该专卖店以前每周共售出![]() 款幼教机器人100个,“双十一”狂购夜中每台
款幼教机器人100个,“双十一”狂购夜中每台![]() 款幼教机器人在标价的基础上降价
款幼教机器人在标价的基础上降价![]() 元,结果这天晚上卖出的
元,结果这天晚上卖出的![]() 款幼教机器人的数量比原来一周卖出的
款幼教机器人的数量比原来一周卖出的![]() 款幼教机器人的数量增加了
款幼教机器人的数量增加了![]() ,同时这天晚上的利润比原来一周的利润增加了
,同时这天晚上的利润比原来一周的利润增加了![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,抛物线y=ax2+bx+c与坐标轴分别交于点A(0,6),B(6,0),C(﹣2,0),点P是线段AB上方抛物线上的一个动点.
(1)求抛物线的解析式;
(2)当点P运动到什么位置时,△PAB的面积有最大值?
(3)过点P作x轴的垂线,交线段AB于点D,再过点P做PE∥x轴交抛物线于点E,连结DE,请问是否存在点P使△PDE为等腰直角三角形?若存在,求出点P的坐标;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的材料:
小凯遇到这样一个问题:如图①,在四边形ABCD中,对角线AC,BD相交于点O,AC=4,BD=6,∠AOB=30°,求四边形ABCD的面积.小凯发现,分别过点A,C作直线BD的垂线,垂足分别为E,F,设AO为m,通过计算△ABD与△BCD的面积和可以使问题得到解决(如图②).请回答:
(1)△ABD的面积为________(用含m的式子表示);
(2)求四边形ABCD的面积.
参考小凯思考问题的方法,解决问题:
如图③,在四边形ABCD中,对角线AC,BD相交于点O,AC=a,BD=b,∠AOB=α(0°<α<90°),则四边形ABCD的面积为________(用含a,b,α的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数y1=![]() 与一次函数y2=k2x+b的图象交于点A(1,8),B(-4,m)两点.
与一次函数y2=k2x+b的图象交于点A(1,8),B(-4,m)两点.
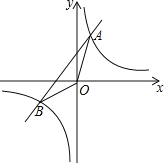
(1)求k1,k2,b的值;
(2)求△AOB的面积;
(3)请直接写出不等式![]() x+b的解.
x+b的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究函数![]() 的图象与性质.小怀根据学习函数的经验,对函数
的图象与性质.小怀根据学习函数的经验,对函数![]() 的图象与性质进行了探究.下面是小怀的探究过程,请补充完成:
的图象与性质进行了探究.下面是小怀的探究过程,请补充完成:
(1)函数![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)列出y与x的几组对应值.请直接写出m的值,m= ;
(3)请在平面直角坐标系xOy中,描出表中各对对应值为坐标的点,并画出该函数的图象;
(4)结合函数的图象,写出函数![]() 的一条性质.
的一条性质.
x | … | ﹣5 | ﹣4 | ﹣3 | ﹣2 | ﹣ | ﹣ | 0 | 1 | 2 | m | 4 | 5 | … |
y | … |
|
|
| 2 | 3 | ﹣1 | 0 |
|
|
|
|
| … |

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场按定价销售某种电器时,每台可获利 48 元,按定价的九折销售该电器 6 台与将定价降低 30 元销售该电器 9 台所获得的利润相等,
(1)该电器每台进价、定价各是多少元?
(2)按(1)的定价该商场一年可销售这种电器 1000 台.经市场调查:每降低一元一年可多卖该种电器出 10 台.如果商场想在一年中使该种电器获利32670 元,那么商场应按几折销售?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com