
【题目】阅读下面的材料:
小凯遇到这样一个问题:如图①,在四边形ABCD中,对角线AC,BD相交于点O,AC=4,BD=6,∠AOB=30°,求四边形ABCD的面积.小凯发现,分别过点A,C作直线BD的垂线,垂足分别为E,F,设AO为m,通过计算△ABD与△BCD的面积和可以使问题得到解决(如图②).请回答:
(1)△ABD的面积为________(用含m的式子表示);
(2)求四边形ABCD的面积.
参考小凯思考问题的方法,解决问题:
如图③,在四边形ABCD中,对角线AC,BD相交于点O,AC=a,BD=b,∠AOB=α(0°<α<90°),则四边形ABCD的面积为________(用含a,b,α的式子表示).

【答案】(1)![]() m;(2)6;解决问题:
m;(2)6;解决问题:![]() absinα.
absinα.
【解析】
(1)首先得出AE的长,再利用三角形的面积公式求出即可;
(2)根据直角三角形的性质可得AE=![]() m,再根据三角形的面积公式可得S△ABD=
m,再根据三角形的面积公式可得S△ABD=![]() BDAE=
BDAE=![]() m,同理再表示CF=
m,同理再表示CF=![]() (4m),然后再表示△BCD的面积,再求两个三角形的面积和可得答案;
(4m),然后再表示△BCD的面积,再求两个三角形的面积和可得答案;
(3)方法与(2)类似.
(1)∵AO=m,∠AOB=30°,
∴AE=![]() m,
m,
∴△ABD的面积为![]() ×
×![]() m×6=
m×6=![]() m.
m.
故答案为![]() m;
m;
(2)由(1)得S△ABD=![]() m,
m,
同理,CF=![]() (4-m),
(4-m),
∴S△BCD=![]() BD·CF=6-
BD·CF=6-![]() m,
m,
∴S四边形ABCD=S△ABD+S△BCD=6;
解决问题:分别过点A,C作直线BD的垂线,垂足分别为E,F,设AO为x,

∵∠AOB=α,
∴AE=x·sinα,
∴S△ABD=![]() BD·AE=
BD·AE=![]() b·x·sinα,
b·x·sinα,
同理,CF=(a-x)·sinα,
∴S△BCD=![]() BD·CF=
BD·CF=![]() b·(a-x)·sinα,
b·(a-x)·sinα,
∴S四边形ABCD=S△ABD+S△BCD=![]() b·x·sinα+
b·x·sinα+![]() b·(a-x)·sinα=
b·(a-x)·sinα=![]() ab·sinα,
ab·sinα,
故答案为![]() ab·sinα.
ab·sinα.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某高中学校为使高一新生入校后及时穿上合身的校服,现提前对某校九年级三班学生即将所穿校服型号情况进行了摸底调查,并根据调查结果绘制了如图两个不完整的统计图(校服型号以身高作为标准,共分为6种型号).

根据以上信息,解答下列问题:
(1)该班共有________名学生.
(2)在条形统计图中,请把空缺部分补充完整.
(3)该班学生所穿校服型号的众数为__________型号,中位数为_________型号.
(4)若该校九年级有学生500人,请你估计穿175型号校服的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在坐标平面中,A(-6,0)、B(6,0),点 C 在 y 轴正半轴上,且∠ACB=90.

⑴求点 C 的坐标;
⑵如图2,点 P 为线段 BC 上一点,连接 PA,设点 P 的横坐标为 m,△PAC 的面积为 S,用含 m 的代数式来表示 S;
⑶如图3,在⑵的条件下,过点 B 向 PA 引垂线,垂足为 E,延长 BE、AC 相交于点 F,连接PF,若 PF=3,求 m 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A(﹣2,1)、B(1,2).

(1)作出点A、B关于x轴的对称点A1、B1,并直接写出A1 、B1 ;
(2)在x轴上找一点P,使PA+PB的值最小,画出点P,并写出点P的坐标;
(3)在如图4×4的正方形网格中,在格点上找一点C,使△ABC为等腰三角形,符合条件的点C的个数为 (直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
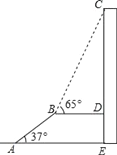
【题目】如图,AB是长为10m,倾斜角为37°的自动扶梯,平台BD与大楼CE垂直,且与扶梯AB的长度相等,在B处测得大楼顶部C的仰角为65°,求大楼CE的高度(结果保留整数).
(参考数据:sin37°≈![]() ,tan37°≈
,tan37°≈![]() ,sin65°≈
,sin65°≈![]() ,tan65°≈
,tan65°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB=60°,半径为2![]() 的⊙M与边OA、OB相切,若将⊙M水平向左平移,当⊙M与边OA相交时,设交点为E和F,且EF=6,则平移的距离为( )
的⊙M与边OA、OB相切,若将⊙M水平向左平移,当⊙M与边OA相交时,设交点为E和F,且EF=6,则平移的距离为( )

A. 2 B. 2或6 C. 4或6 D. 1或5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,F为EC的中点,连接AF.写出AF与BD的数量关系和位置关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,∠ACB=30°,AC=10,CD是角平分线.
(1)如图1,若E是AC边上的一个定点,在CD上找一点P,使PA+PE的值最小;
(2)如图2,若E是AC边上的一个动点,在CD上找一点P,使PA+PE的值最小,并直接写出其最小值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com