
【题目】如图,△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,F为EC的中点,连接AF.写出AF与BD的数量关系和位置关系,并说明理由.

【答案】AF=![]() BD,AF⊥BD,理由见解析.
BD,AF⊥BD,理由见解析.
【解析】
过点C作CG∥AE交直线AF于G,直线AF交BD于H,证明△CGF≌△EAF(AAS),得出CG=AE,AF=GF,得出AF=![]() AG,证明△BAD≌△ACG(SAS),得出BD=AG,∠ABD=∠CAG,进而得出结论.
AG,证明△BAD≌△ACG(SAS),得出BD=AG,∠ABD=∠CAG,进而得出结论.
AF=![]() BD,AF⊥BD,理由如下:
BD,AF⊥BD,理由如下:
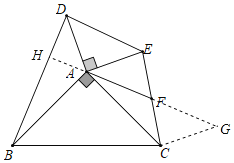
过点C作CG∥AE交直线AF于G,直线AF交BD于H,如图所示:
则∠G=∠EAF,∠EAC+∠ACG=180°,
∵F为EC的中点,
∴CF=EF,
在△CGF和△EAF中,
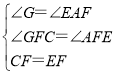 ,
,
∴△CGF≌△EAF(AAS),
∴CG=AE,AF=GF,
∴AF=![]() AG,
AG,
∵△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,
∴AB=AC,AD=AE,∠EAC+∠BAD=360°-90°-90°=180°,∠CAG+∠BAH=90°,
∴AD=CG,∠BAD=∠ACG,
在△BAD和△ACG中,
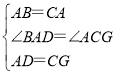 ,
,
∴△BAD≌△ACG(SAS),
∴BD=AG,∠ABD=∠CAG,
∴AF=![]() BD,∠ABD+∠BAH=90°,
BD,∠ABD+∠BAH=90°,
∴AF⊥BD.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,给出下列结论:
①b2=4ac;②abc>0;③a>c;④4a﹣2b+c>0,其中正确的个数有( )

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 方格纸上的两条对称轴
方格纸上的两条对称轴![]() 、
、![]() 相交于中心点
相交于中心点![]() ,将格点
,将格点![]() (顶点在小正方形的顶点上)分别作下列三种变换:
(顶点在小正方形的顶点上)分别作下列三种变换:

①先以点![]() 为中心顺时针旋转
为中心顺时针旋转![]() ,再向右平移
,再向右平移![]() 格,最后向上平移
格,最后向上平移![]() 格;
格;
②先以点![]() 为中心作中心对称图形,再以点
为中心作中心对称图形,再以点![]() 的对应点为中心逆时针旋转
的对应点为中心逆时针旋转![]() ;
;
③先以直线![]() 为轴作轴对称图形,再向上平移
为轴作轴对称图形,再向上平移![]() 格,最后以点
格,最后以点![]() 的对应点为中心顺时针旋转
的对应点为中心顺时针旋转![]() .
.
其中,能将![]() 变换成
变换成![]() 的种数是( )
的种数是( )
A. 0种 B. 1种 C. 2种 D. 3种
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的材料:
小凯遇到这样一个问题:如图①,在四边形ABCD中,对角线AC,BD相交于点O,AC=4,BD=6,∠AOB=30°,求四边形ABCD的面积.小凯发现,分别过点A,C作直线BD的垂线,垂足分别为E,F,设AO为m,通过计算△ABD与△BCD的面积和可以使问题得到解决(如图②).请回答:
(1)△ABD的面积为________(用含m的式子表示);
(2)求四边形ABCD的面积.
参考小凯思考问题的方法,解决问题:
如图③,在四边形ABCD中,对角线AC,BD相交于点O,AC=a,BD=b,∠AOB=α(0°<α<90°),则四边形ABCD的面积为________(用含a,b,α的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)方程x2﹣3x+2=0的解是
(2)有两个可以自由转动的均匀转盘A,B都被分成了3等份,并在每一份内均标有数字,如图所示,规则如下:①分别转动转盘A,B;②两个转盘停止后,观察两个指针所指份内的数字(若指针停在等分线上,那么重转一次,直到指针指向某一份内为止).用列表法(或树状图)分别求出“两个指针所指的数字都是方程x2﹣3x+2=0的解”的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边△ABC中,D是△ABC内一点,且DA=DB,E为△ABC外一点,连接BE交AC于F,BE=BC,BD平分∠EBC,连接DE,CE,AD∥CE.
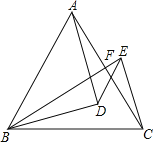
(1)求证:∠DAC=∠DBE;
(2)若AB=6,求△BEC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程![]() 。
。
(1)求证:方程有两个不相等的实数根;
(2)若△ABC的两边AB、AC的长是方程的两个实数根,第三边BC的长为5。当△ABC是等腰三角形时,求k的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com