
【题目】在等边△ABC中,D是△ABC内一点,且DA=DB,E为△ABC外一点,连接BE交AC于F,BE=BC,BD平分∠EBC,连接DE,CE,AD∥CE.
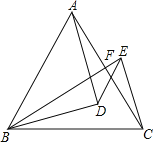
(1)求证:∠DAC=∠DBE;
(2)若AB=6,求△BEC的面积.
【答案】(1)见解析;(2)△BEC的面积=9.
【解析】
(1)连接CD,先证△BDC≌△ADC,可得∠DAC=∠DBC,又因为BD平分∠EBC,可得∠DBC=∠DBE,即可证得∠DAC=∠DBE;
(2)先证△BDE≌△BDC;又因为△ADC≌△BDC,可得∠BED=30°,再证∠BHC=90°,从而证得∠ACE=∠DBC=15°,可证∠CFB=90°,在求面积即可.
(1)连接CD,延长BD交EC于点H,

∵△ABC是等边三角形,
∴AC=BC,∠ACB=60°,
∵AC=BC,CD=CD,AD=BD,
∴△ADC≌△BDC(SSS)
∴∠DAC=∠DBC,
∵BD平分∠EBC,
∴∠DBC=∠DBE,
∴DAC=∠DBE;
(2)∵BE=BC,∠DBC=∠DBE,BD=BD,
∴△BDE≌△BDC(SAS)
∴∠BED=∠BCD,
∵△ADC≌△BDC
∴∠BCD=∠ACD=30°,
∴∠BED=30°,
∵AD∥CE,
∴∠DAC=∠ACE=∠DBC=∠DBE,
∵BE=BC,∠DBC=∠DBE,
∴∠BHC=90°,
∴∠DBC+∠ACB+∠ACE=90°,
∴∠ACE=∠DBC=15°,
∴∠EBC=30°,
∴∠CFB=90°,
∴CF=![]() BC=3,
BC=3,
∴△BEC的面积=![]() ×BE×CF=9.
×BE×CF=9.


科目:初中数学 来源: 题型:
【题目】如图,直线MN分别与直线AC、DG交于点B.F,且∠1=∠2.∠ABF的角平分线BE交直线DG于点E,∠BFG的角平分线FC交直线AC于点C.

(1)求证:BE∥CF;
(2)若∠C=35°,求∠BED的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
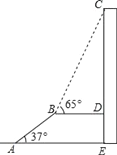
【题目】如图,AB是长为10m,倾斜角为37°的自动扶梯,平台BD与大楼CE垂直,且与扶梯AB的长度相等,在B处测得大楼顶部C的仰角为65°,求大楼CE的高度(结果保留整数).
(参考数据:sin37°≈![]() ,tan37°≈
,tan37°≈![]() ,sin65°≈
,sin65°≈![]() ,tan65°≈
,tan65°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,F为EC的中点,连接AF.写出AF与BD的数量关系和位置关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
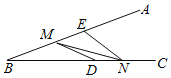
【题目】如图,∠ABC=20°,点D,E分别在射线BC,BA上,且BD=3,BE=3,点M,N分别是射线BA,BC上的动点,求DM+MN+NE的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,灯杆AB与墙MN的距离为18米,小丽在离灯杆(底部)9米的D处测得其影长DE为3m,设小丽身高为1.6m.
(1)求灯杆AB的高度;
(2)小丽再向墙走7米,她的影子能否完全落在地面上?若能,求此时的影长;若不能,求落在墙上的影长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学活动课上,老师提出这样一个问题:“已知![]() ,同学们只用一块三角板可以画出它的角平分线吗?”聪明的小阳经过思考设计了如下方案(如图):
,同学们只用一块三角板可以画出它的角平分线吗?”聪明的小阳经过思考设计了如下方案(如图):
(1)在角的两边OM、ON上分别取OA=OB;
(2)过点A作DA⊥OM于点A,交ON于点D;过点B作EB⊥ON于点B,交OM于点E,AD、BE交于点C;
(3)作射线OC.
小阳接着解释说:“此时,△OAC≌△OBC,所以射线OC为∠MON的平分线。”小阳的方案中,△OAC≌△OBC的依据是( )

A.SASB.ASAC.HLD.AAS
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用同样规格的规格黑白两色正方形瓷砖铺设矩形地面,请观察图形并解答有关问题.

![]() 在第
在第![]() 个图中,每一横行共有________块瓷砖,每竖行共有________块瓷砖(均用含
个图中,每一横行共有________块瓷砖,每竖行共有________块瓷砖(均用含![]() 的代数式表示)
的代数式表示)
![]() 设铺设地面所用的瓷砖总块数
设铺设地面所用的瓷砖总块数![]() ,写出
,写出![]() 与
与![]() 的函数关系式(不写
的函数关系式(不写![]() 的取值范围)
的取值范围)
![]() 按上述铺设方案,铺一块这样的地面共用了
按上述铺设方案,铺一块这样的地面共用了![]() 块瓷砖,求此时
块瓷砖,求此时![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com