
【题目】如图,在△AOB中,∠AOB=90°,点A的坐标为(4,2),BO=4![]() ,反比例函数y=
,反比例函数y=![]() 的图象经过点B,则k的值为_____.
的图象经过点B,则k的值为_____.

【答案】﹣32
【解析】
根据∠AOB=90°,过点A作AC⊥x轴,过点B作BD⊥x轴,证明△DBO∽△COA,再利用相似三角形的对应边成比例,列出比例式进行计算,求得点B的坐标,进而得出k的值.
过点A作AC⊥x轴,过点B作BD⊥x轴,垂足分别为C、D,则∠OCA=∠BDO=90°,
∴∠DBO+∠BOD=90°,
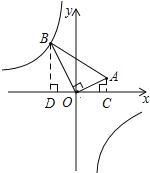
∵∠AOB=90°,
∴∠AOC+∠BOD=90°,
∴∠DBO=∠AOC,
∴△DBO∽△COA,
∴![]() ,
,
∵点A的坐标为(4,2),
∴AC=2,OC=4,
∴AO=![]() ,
,
∴![]() ,即BD=8,DO=4,
,即BD=8,DO=4,
∴B(-4,8),
∵反比例函数y=![]() 的图象经过点B,
的图象经过点B,
∴k的值为-4×8=-32.
故答案为:-32.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
【题目】阅读下面的材料:
小凯遇到这样一个问题:如图①,在四边形ABCD中,对角线AC,BD相交于点O,AC=4,BD=6,∠AOB=30°,求四边形ABCD的面积.小凯发现,分别过点A,C作直线BD的垂线,垂足分别为E,F,设AO为m,通过计算△ABD与△BCD的面积和可以使问题得到解决(如图②).请回答:
(1)△ABD的面积为________(用含m的式子表示);
(2)求四边形ABCD的面积.
参考小凯思考问题的方法,解决问题:
如图③,在四边形ABCD中,对角线AC,BD相交于点O,AC=a,BD=b,∠AOB=α(0°<α<90°),则四边形ABCD的面积为________(用含a,b,α的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)方程x2﹣3x+2=0的解是
(2)有两个可以自由转动的均匀转盘A,B都被分成了3等份,并在每一份内均标有数字,如图所示,规则如下:①分别转动转盘A,B;②两个转盘停止后,观察两个指针所指份内的数字(若指针停在等分线上,那么重转一次,直到指针指向某一份内为止).用列表法(或树状图)分别求出“两个指针所指的数字都是方程x2﹣3x+2=0的解”的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边△ABC中,D是△ABC内一点,且DA=DB,E为△ABC外一点,连接BE交AC于F,BE=BC,BD平分∠EBC,连接DE,CE,AD∥CE.
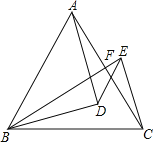
(1)求证:∠DAC=∠DBE;
(2)若AB=6,求△BEC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程![]() 。
。
(1)求证:方程有两个不相等的实数根;
(2)若△ABC的两边AB、AC的长是方程的两个实数根,第三边BC的长为5。当△ABC是等腰三角形时,求k的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年8月.山西龙城将迎来全国第二届青年运动会,盛会将至,整个城市已经进入了全力准备的状态.太职学院足球场作为一个重要比赛场馆.占地面积约24300平方米.总建筑面积4790平方米,设有2476个座位,整体建筑简洁大方,独具特色.2018年3月15日该场馆如期开工,某施工队负责安装该场馆所有座位,在安装完476个座位后,采用新技术,效率比原来提升了![]() .结来比原计划提前4天完成安装任务.求原计划每天安装多少个座位.
.结来比原计划提前4天完成安装任务.求原计划每天安装多少个座位.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”“10元”“20元”“30元”的字样.规定:顾客在本超市一次性消费满200元,就可以在箱子里先后摸出2个小球(第一次摸出后不放回).某顾客刚好消费200元,则该顾客所获得购物券的金额不低于30元的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com