
【题目】如图,已知∠AOB=60°,半径为2![]() 的⊙M与边OA、OB相切,若将⊙M水平向左平移,当⊙M与边OA相交时,设交点为E和F,且EF=6,则平移的距离为( )
的⊙M与边OA、OB相切,若将⊙M水平向左平移,当⊙M与边OA相交时,设交点为E和F,且EF=6,则平移的距离为( )

A. 2 B. 2或6 C. 4或6 D. 1或5
【答案】B
【解析】
本题分圆心M在OA的左边和右边两种情况求解即可.
当将⊙M水平向左平移,当点M运动到M′位置时,如图1:
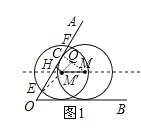
作MC⊥OA于C点,M′H⊥OA于H,M′Q⊥MC于Q,连结M′E,
∵⊙M与边OB、OA相切,
∴MM′∥OB,MC=2![]() ,
,
∵M′H⊥OA,
∴EH=FH=![]() EF=
EF=![]() ×6=3,
×6=3,
在Rt△EHM′中,EM′=2![]() ,
,
∴HM′=![]() =
= ![]() ,
,
∵M′Q⊥MC,
∴四边形M′QCH为矩形,
∴CQ=M′H=![]() ,
,
∴MQ=2![]() -
-![]() =
=![]() ,
,
∵∠QM′M=∠AOB=60°,
∴∠QM′M=30°,
∴M′Q=![]() MQ=1,
MQ=1,
∴MM′=2;
当将⊙M水平向左平移,当点M运动到M″位置时,如图2,
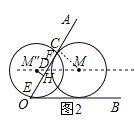
作MC⊥OA于C点,M″H⊥OA于H,M″M交OA于D点,
易得MC=2![]() ,M″H=
,M″H=![]() ,
,
∵∠MDC=∠M″DH=∠AOB=60°,
∴∠HM″D=30°,∠CMD=30°,
在Rt△CDM中,CM=2![]() ,则DC=2, DM=4,
,则DC=2, DM=4,
在Rt△HM″D中,M″H =![]() ,则DH=1,M″D=2,
,则DH=1,M″D=2,
∴MM″= DM+ M″D =4+2=6,
综上所述,当⊙M平移的距离为2或6.故选:B.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
【题目】某商场经销一种商品,已知其每件进价为40元。现在每件售价为70元,每星期可卖出500件。该商场通过市场调查发现:若每件涨价1元,则每星期少卖出10件;若每件降价1元,则每星期多卖出m(m为正整数)件。设调查价格后每星期的销售利润为W元。
(1)设该商品每件涨价x(x为正整数)元,
①若x=5,则每星期可卖出____件,每星期的销售利润为_____元;
②当x为何值时,W最大,W的最大值是多少。
(2)设该商品每件降价y(y为正整数)元,
①写出W与Y的函数关系式,并通过计算判断:当m=10时每星期销售利润能否达到(1)中W的最大值;
②若使y=10时,每星期的销售利润W最大,直接写出W的最大值为_____。
(3)若每件降价5元时的每星期销售利润,不低于每件涨价15元时的每星期销售利润,求m的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,轮船沿正南方向以30海里/时的速度匀速航行,在M处观测到灯塔P在南偏西22°方向上.航行2小时后到达N处,观测灯塔P在南偏西44°方向上,若该船继续向南航行至离灯塔最近的位置,则此时轮船离灯塔的距离约为(参考数据:sin68°≈0.9272,sin46°≈0.7193,sin22°≈0.3746,sin44°≈0.6947)( )

A. 22.48海里 B. 41.68海里
C. 43.16海里 D. 55.63海里
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的材料:
小凯遇到这样一个问题:如图①,在四边形ABCD中,对角线AC,BD相交于点O,AC=4,BD=6,∠AOB=30°,求四边形ABCD的面积.小凯发现,分别过点A,C作直线BD的垂线,垂足分别为E,F,设AO为m,通过计算△ABD与△BCD的面积和可以使问题得到解决(如图②).请回答:
(1)△ABD的面积为________(用含m的式子表示);
(2)求四边形ABCD的面积.
参考小凯思考问题的方法,解决问题:
如图③,在四边形ABCD中,对角线AC,BD相交于点O,AC=a,BD=b,∠AOB=α(0°<α<90°),则四边形ABCD的面积为________(用含a,b,α的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,CF⊥AC交AB的延长线于点F,G为BC的中点,射线AG交CF于D,E在CF上,CE=AD,连接BD,BE.求证:△BDE是等边三角形

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)方程x2﹣3x+2=0的解是
(2)有两个可以自由转动的均匀转盘A,B都被分成了3等份,并在每一份内均标有数字,如图所示,规则如下:①分别转动转盘A,B;②两个转盘停止后,观察两个指针所指份内的数字(若指针停在等分线上,那么重转一次,直到指针指向某一份内为止).用列表法(或树状图)分别求出“两个指针所指的数字都是方程x2﹣3x+2=0的解”的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场有A,B两种商品,若买2件A商品和1件B商品,共需80元;若买3件A商品和2件B商品,共需135元.
(1)设A,B两种商品每件售价分别为a元、b元,求a、b的值;
(2)B商品每件的成本是20元,根据市场调查:若按(1)中求出的单价销售,该商场每天销售B商品100件;若销售单价每上涨1元,B商品每天的销售量就减少5件.
①求每天B商品的销售利润y(元)与销售单价(x)元之间的函数关系?
②求销售单价为多少元时,B商品每天的销售利润最大,最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com