
【题目】某商场经销一种商品,已知其每件进价为40元。现在每件售价为70元,每星期可卖出500件。该商场通过市场调查发现:若每件涨价1元,则每星期少卖出10件;若每件降价1元,则每星期多卖出m(m为正整数)件。设调查价格后每星期的销售利润为W元。
(1)设该商品每件涨价x(x为正整数)元,
①若x=5,则每星期可卖出____件,每星期的销售利润为_____元;
②当x为何值时,W最大,W的最大值是多少。
(2)设该商品每件降价y(y为正整数)元,
①写出W与Y的函数关系式,并通过计算判断:当m=10时每星期销售利润能否达到(1)中W的最大值;
②若使y=10时,每星期的销售利润W最大,直接写出W的最大值为_____。
(3)若每件降价5元时的每星期销售利润,不低于每件涨价15元时的每星期销售利润,求m的取值范围。
【答案】(1)①450,15750;②x=10,最大值为16000;(2)①不能,理由见解析; ②20000元;(3)m≥26
【解析】试题分析:![]() ①直接进行计算即可.
①直接进行计算即可.
②根据利润=每件的利润![]() 销售量即可写出函数关系式,进而求得利润的最大值.
销售量即可写出函数关系式,进而求得利润的最大值.
![]() ①根据利润=每件的利润
①根据利润=每件的利润![]() 销售量写出
销售量写出![]() 与
与![]() 的关系式,根据二次函数的性质求出最大值和
的关系式,根据二次函数的性质求出最大值和![]() 中的最大值进行比较即可.
中的最大值进行比较即可.
②直接写出最大利润即可.
![]() 根据题意,列出不等式,解不等式即可.
根据题意,列出不等式,解不等式即可.
试题解析:(1)①当![]() 时,每星期可卖出:
时,每星期可卖出:![]() 件,
件,
每星期的销售利润为:![]() 元.
元.
故答案为:![]()
②根据题意得:![]()
W=![]() ,
,
∵W是x的二次函数,且-10<0,
∴当![]() 时,W最大,
时,W最大,
W最大值=![]() ,
,
答:当x=10时,W最大,最大值为16000.
(2)①W=(70-40-y)(500+my),
W=![]() ,
,
当m=10时,W=![]() ,
,
∵W是y的二次函数,且-10<0,
∴当y=![]() 时,W最大,当y>-10时,W随y的增大而减小,
时,W最大,当y>-10时,W随y的增大而减小,
∵y为正整数,
∴当y=1时,W最大,W最大=-10-200+15000=14790,
14790<16000
答:销售利润不能达到(1)中W的最大值,
②当![]() 时,即
时,即![]() 解得:
解得:![]()
此时,![]() 元.
元.
故答案为:20000元.
(3)降价5元时销售利润为:W=(70-40-5)(500+5m)=125m+125000,
涨价15元时的销售利润为:W=![]() +3000+15000=15750,
+3000+15000=15750,
根据题意,得125m+12500≥15750,
解得:m≥26,
答:m的取值范围是m≥26.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:
【题目】定理描述
(1)如图1,用文字语言或符号语言叙述三角形中位线性质定理的内容.
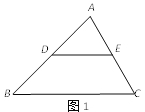
.
证法回顾
证明三角形中位线性质定理的方法很多,但多数都需要通过添加辅助线构图去完成.下列是其中一种证法的添加辅助线方法:
添加辅助线,如图2,在△ABC中,过点C作CF∥AB,与DE的延长线交于点F.
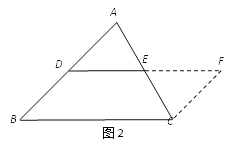
(2)上述证法中,证明三角形中位线定理中的DE∥BC的依据是( )
A.同位角相等,两直线平行.
B.平行四边形对边平行.
C.同旁内角互补,两直线平行.
D.平行于同一条直线的两条直线互相平行
拓展延伸
(3)利用证明三角形中位线定理获得的经验解决下面的问题:
如图3,在△ABC中,∠B=45°,AB=10,BC=8,DE是△ABC的中位线,过点D、E作DF∥EG,分别交BC于F、G,过点A作MN∥BC,分别与FD、GE的延长线交于M、N,则四边形MFGN周长的最小值是
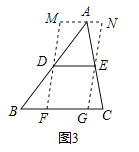
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解甲、乙两班英语口语水平,每班随机抽取了10名学生进行了口语测验,测验成绩满分为10分,参加测验的10名学生成绩(单位:分)称为样本数据,抽样调查过程如下:
收集数据
甲、乙两班的样本数据分别为:
甲班:6 7 9 4 6 7 6 9 6 10
乙班:7 8 9 7 5 7 8 5 9 5
整理和描述数据
规定了四个层次:9分以上(含9分)为“优秀”,8-9分(含8分)为“良好”,6-8分(含6分)为“一般”,6分以下(不含6分)为“不合格”。按以上层次分布绘制出如下的扇形统计图。

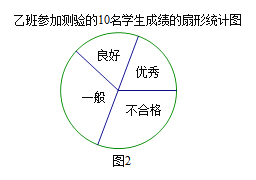
请计算:(1)图1中,“不合格”层次所占的百分比;
(2)图2中,“优秀”层次对应的圆心角的度数。
分析数据
对于甲、乙两班的样本数据,请直接回答:
(1)甲班的平均数是7,中位数是_____;乙班的平均数是_____,中位数是7;
(2)从平均数和中位数看,____班整体成绩更好。
解决问题
若甲班50人,乙班40人,通过计算,估计甲、乙两班“不合格”层次的共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工厂加工某种茶叶,计划一周生产![]() 千克,平均每天生产
千克,平均每天生产![]() 千克,由于各种原因实际每天产量与计划量相比有出入,某周七天的生产情况记录如下(超产为正、减产为负):
千克,由于各种原因实际每天产量与计划量相比有出入,某周七天的生产情况记录如下(超产为正、减产为负):
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(![]() )这一周的实际产量是多少千克?
)这一周的实际产量是多少千克?
(![]() )该厂规定工人工资参照平均产量计发,每千克
)该厂规定工人工资参照平均产量计发,每千克![]() 元.若超产,则超产的部分每千克
元.若超产,则超产的部分每千克![]() 元;若低于平均产量,按实际产量计发,而且每少
元;若低于平均产量,按实际产量计发,而且每少![]() 千克扣除
千克扣除![]() 元,那么该工厂工人这一周的工资总额是多少?
元,那么该工厂工人这一周的工资总额是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
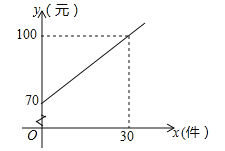
【题目】某快递公司的每位“快递小哥”日收入与每日的派送量成一次函数关系,如图所示.
(1)求每位“快递小哥”的日收入y(元)与日派送量x(件)之间的函数关系式;
(2)已知某“快递小哥”的日收入不少于110元,则他至少要派送多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】情境观察:

如图1,△ABC中,AB=AC,∠BAC=45°,CD⊥AB,AE⊥BC,垂足分别为D、E,CD与AE交于点F.
①写出图1中所有的全等三角形 ;
②线段AF与线段CE的数量关系是 .
问题探究:
如图2,△ABC中,∠BAC=45°,AB=BC,AD平分∠BAC,AD⊥CD,垂足为D,AD与BC交于点E.
求证:AE=2CD.
拓展延伸:
如图3,△ABC中,∠BAC=45°,AB=BC,点D在AC上,∠EDC=![]() ∠BAC,DE⊥CE,垂足为E,DE与BC交于点F.求证:DF=2CE.
∠BAC,DE⊥CE,垂足为E,DE与BC交于点F.求证:DF=2CE.
要求:请你写出辅助线的作法,并在图3中画出辅助线,不需要证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
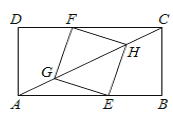
【题目】如图,矩形ABCD中,AB=8,BC=6.点E在边AB上,点F在边CD上,点G、H在对角线AC上,若四边形EGFH是菱形,则AE的长是_________________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工厂接到订单,需要边长为(a+3)和3的两种正方形卡纸.
(1)仓库只有边长为(a+3)的正方形卡纸,现决定将部分边长为(a+3)的正方形纸片,按图甲所示裁剪得边长为3的正方形.
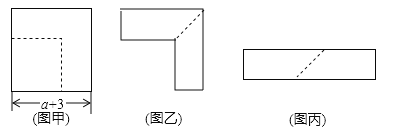
①如图乙,求裁剪正方形后剩余部分的面积(用含a代数式来表示);
②剩余部分沿虚线又剪拼成一个如图丙所示长方形(不重叠无缝隙),则拼成的长方形的边长多少?(用含a代数式来表示);
(2)若将裁得正方形与原有正方形卡纸放入长方体盒子底部,按图1,图2两种方式放置(图1,图2中两张正方形纸片均有部分重叠),盒子底部中未被这两张正方形纸片覆盖的部分用阴影表示,设图1中阴影部分的面积为S1,图2中阴影部分的面积为S2测得盒子底部长方形长比宽多3,则S2﹣S1的值为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com