
【题目】定理描述
(1)如图1,用文字语言或符号语言叙述三角形中位线性质定理的内容.
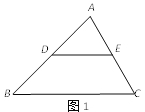
.
证法回顾
证明三角形中位线性质定理的方法很多,但多数都需要通过添加辅助线构图去完成.下列是其中一种证法的添加辅助线方法:
添加辅助线,如图2,在△ABC中,过点C作CF∥AB,与DE的延长线交于点F.
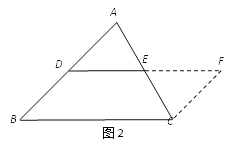
(2)上述证法中,证明三角形中位线定理中的DE∥BC的依据是( )
A.同位角相等,两直线平行.
B.平行四边形对边平行.
C.同旁内角互补,两直线平行.
D.平行于同一条直线的两条直线互相平行
拓展延伸
(3)利用证明三角形中位线定理获得的经验解决下面的问题:
如图3,在△ABC中,∠B=45°,AB=10,BC=8,DE是△ABC的中位线,过点D、E作DF∥EG,分别交BC于F、G,过点A作MN∥BC,分别与FD、GE的延长线交于M、N,则四边形MFGN周长的最小值是
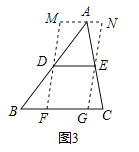
【答案】(1)见解析;(2)B;(3)见解析.
【解析】
(1)分别运用文字语言和符号语言表述即可;
(2)作出图形,然后写出已知、求证,延长DE到F,使DE=EF,利用“边角边”证明△ADE和△CEF全等,根据全等三角形对应边相等可得AD=CF,全等三角形对应角相等可得∠F=∠ADE,再求出BD=CF,根据内错角相等,两直线平行判断出AB∥CF,然后判断出四边形BCFD是平行四边形,根据平行四边形的性质可得DF∥BC,DF=BC;
(3)先判断出四边形MFGN是平行四边形,再判断出MN=FG=DE=4,进而判断出MF⊥BC时,四边形MFGN的周长最小,最后构造出直角三角形求出AH即可得出结论.
(1)文字语言:三角形的中位线平行于第三边,并且等于第三边的一半;
符号语言:∵DE是△ABC的中位线,∴DE=![]() BC, DE∥BC
BC, DE∥BC
(2)已知:△ABC中,点D、E分别是AB、AC的中点,
求证:DE=![]() BC,DE∥BC,
BC,DE∥BC,
证明:如图,延长DE到F,使DE=EF,连接CF,

∵点E是AC的中点,
∴AE=CE,
在△ADE和△CEF中,
 ,
,
∴△ADE≌△CEF(SAS),
∴AD=CF,∠ADE=∠F,
∴AB∥CF,
∵点D是AB的中点,
∴AD=BD,
∴BD=CF,
∴BD∥CF,
∴四边形BCFD是平行四边形,
∴DF∥BC,DF=BC,
∴DE∥BC且DE=![]() BC.
BC.
故答案为:B.
(3)如图,

∵MN∥BC,FM∥GN,
∴四边形MFGN是平行四边形,
∴MF=NG,MN=FG,
∵DE是△ABC的中位线,
∴DE=![]() BC=4,DE∥BC,
BC=4,DE∥BC,
∴MN=FG=![]() BC=4,
BC=4,
∴四边形MFGN周长=2(MF+FG)=2MF+8,
∴MF⊥BC时,MF最短,
即:四边形MFGN的周长最小,
过点A作AH⊥BC于H,
∴FM=AH
在Rt△ABH中,∠B=45°,AB=10,
∴AH=![]() =5
=5![]() ,
,
∴四边形MFGN的周长最小为2MF+8=10![]() +8.
+8.
故答案为10![]() +8.
+8.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知数轴上两点![]() ,
,![]() 对应的数分别为
对应的数分别为![]() ,8.
,8.
(1)如图1,如果点![]() 和点
和点![]() 分别从点
分别从点![]() ,
,![]() 同时出发,沿数轴负方向运动,点
同时出发,沿数轴负方向运动,点![]() 的运动速度为每秒2个单位,点
的运动速度为每秒2个单位,点![]() 的运动速度为每秒6个单位.
的运动速度为每秒6个单位.

①![]() ,
,![]() 两点之间的距离为__________.
两点之间的距离为__________.
②当![]() ,
,![]() 两点相遇时,点
两点相遇时,点![]() 在数轴上对应的数是____________.
在数轴上对应的数是____________.
③求点![]() 出发多少秒后,与点
出发多少秒后,与点![]() 之间相距4个单位长度?
之间相距4个单位长度?
(2)如图2,如果点![]() 从点
从点![]() 出发沿数轴的正方向以每秒2个单位的速度运动,点
出发沿数轴的正方向以每秒2个单位的速度运动,点![]() 、
、![]() 分别是线段
分别是线段![]() 、
、![]() 的中点,在运动过程中,线段
的中点,在运动过程中,线段![]() 的长度是否为定值.如果变化,请说明理由:如果不变,请直接写出线段
的长度是否为定值.如果变化,请说明理由:如果不变,请直接写出线段![]() 的长度.
的长度.
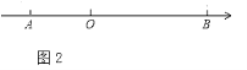
查看答案和解析>>
科目:初中数学 来源: 题型:
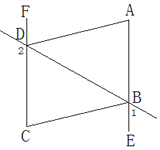
【题目】如图,∠1+∠2=180°,∠DAE=∠BCF,DA平分∠BDF.
(1)AE与FC会平行吗?说明理由.
(2)AD与BC的位置关系如何?为什么?
(3)求证:BC平分∠DBE.
查看答案和解析>>
科目:初中数学 来源: 题型:
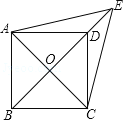
【题目】如图,已知平行四边形ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且△ACE是等边三角形.
(1)求证:四边形ABCD是菱形;
(2)若∠AED=2∠EAD,求证:四边形ABCD是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明收集了某品牌运动鞋的鞋标,如图所示.

为了搞清楚这些字母、数字的含义,他以“鞋码”为关键词上网搜索,得到相关资料如下:cm表示以厘米为单位的脚长;US表示美制鞋码,UK表示英制鞋码,EUR表示欧洲鞋码.一个关于欧州鞋码的介绍中还有这么一句话:“欧洲鞋码=1.5×脚长+2,单位:cm”.
(1)如果脚长用a表示,请用含a的代数式表示欧洲鞋码;有一个脚长为24cm的人想购买鞋子,应建议他选择EUR码对应数字为多少?
(2)小明发现乙、丙两个鞋标显示的cm数不同,但是US码对应数字都是6.5,显然其中一个鞋标是假的.从欧洲鞋码与脚长的换算经验,US码与cm数应该也存在某种关系.若cm数用b表示,请用含b的代数式表示出US码,并帮助小明判断乙、丙中哪个鞋标为假鞋标?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一条笔直公路BD的正上方A处有一探测仪,AD=24m,∠D=90°,一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50°.
(Ⅰ)求B,C两点间的距离(结果精确到1m);
(Ⅱ)若规定该路段的速度不得超过15m/s,判断此轿车是否超速.
参考数据:tan31°≈0.6,tan50°≈1.2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,![]() 的顶点均在格点上,点
的顶点均在格点上,点![]() 的坐标为
的坐标为![]() .
.

①把![]() 向上平移5个单位后得到对应的
向上平移5个单位后得到对应的![]() ,画出
,画出![]() ,并写出
,并写出![]() 的坐标;
的坐标;
②以原点![]() 为对称中心,画出
为对称中心,画出![]() 与关于原点
与关于原点![]() 对称的
对称的![]() ,并写出点
,并写出点![]() 的坐标.
的坐标.
③以原点O为旋转中心,画出把![]() 顺时针旋转90°的图形△A3B3C3,并写出C3的坐标.
顺时针旋转90°的图形△A3B3C3,并写出C3的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过正方形ABCD的顶点D作DE∥AC交BC的延长线于点E.
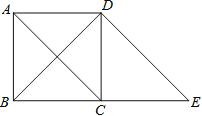
(1)判断四边形ACED的形状,并说明理由;
(2)若BD=8cm,求线段BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场经销一种商品,已知其每件进价为40元。现在每件售价为70元,每星期可卖出500件。该商场通过市场调查发现:若每件涨价1元,则每星期少卖出10件;若每件降价1元,则每星期多卖出m(m为正整数)件。设调查价格后每星期的销售利润为W元。
(1)设该商品每件涨价x(x为正整数)元,
①若x=5,则每星期可卖出____件,每星期的销售利润为_____元;
②当x为何值时,W最大,W的最大值是多少。
(2)设该商品每件降价y(y为正整数)元,
①写出W与Y的函数关系式,并通过计算判断:当m=10时每星期销售利润能否达到(1)中W的最大值;
②若使y=10时,每星期的销售利润W最大,直接写出W的最大值为_____。
(3)若每件降价5元时的每星期销售利润,不低于每件涨价15元时的每星期销售利润,求m的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com