
【题目】如图,在一条笔直公路BD的正上方A处有一探测仪,AD=24m,∠D=90°,一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50°.
(Ⅰ)求B,C两点间的距离(结果精确到1m);
(Ⅱ)若规定该路段的速度不得超过15m/s,判断此轿车是否超速.
参考数据:tan31°≈0.6,tan50°≈1.2.

 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案科目:初中数学 来源: 题型:
【题目】有依次3个数:2、9、7.对任意相邻的两个数,都用右边的数减去左边的数,所得之差写在这两个数之间,可产生一个新数串:2、7、9、-2、7,这称为第1次操作,做第2次同样的操作后也可以产生一个新数串:2、5、7、2、9、-11、-2、9、7,继续依次操作下去,问从数串2、9、7开始操作第20次后所产生的那个数串的所有数之和是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,∠A0B=420,点P为∠A0B内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,P1P2=15,则△PMN的周长为________,∠MPN ________.
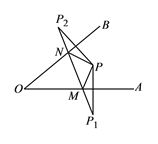
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们已经学习过反比例函数y=![]() 的图像和性质,请你回顾研究它的过程,运用所学知识对函数y=
的图像和性质,请你回顾研究它的过程,运用所学知识对函数y=![]() 的图像和性质进行探索,并解决下列问题:
的图像和性质进行探索,并解决下列问题:
(1)该函数的图像大致是( )
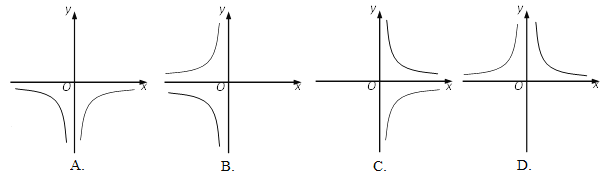
(2)写出该函数两条不同类型的性质:
① ;
② .
(3)写出不等式![]() -3>0的解集.
-3>0的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
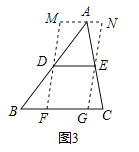
【题目】定理描述
(1)如图1,用文字语言或符号语言叙述三角形中位线性质定理的内容.
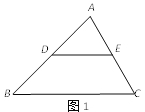
.
证法回顾
证明三角形中位线性质定理的方法很多,但多数都需要通过添加辅助线构图去完成.下列是其中一种证法的添加辅助线方法:
添加辅助线,如图2,在△ABC中,过点C作CF∥AB,与DE的延长线交于点F.
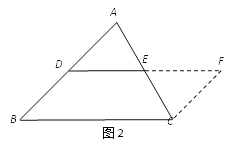
(2)上述证法中,证明三角形中位线定理中的DE∥BC的依据是( )
A.同位角相等,两直线平行.
B.平行四边形对边平行.
C.同旁内角互补,两直线平行.
D.平行于同一条直线的两条直线互相平行
拓展延伸
(3)利用证明三角形中位线定理获得的经验解决下面的问题:
如图3,在△ABC中,∠B=45°,AB=10,BC=8,DE是△ABC的中位线,过点D、E作DF∥EG,分别交BC于F、G,过点A作MN∥BC,分别与FD、GE的延长线交于M、N,则四边形MFGN周长的最小值是
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于50%.经试销发现,销售量P(件)与销售单价x(元)符合一次函数关系,当销售单价为65元时销售量为55件,当销售单价为75元时销售量为45件.
(Ⅰ)求P与x的函数关系式;
(Ⅱ)若该商场获得利润为y元,试写出利润y与销售单价x之间的关系式;
(Ⅲ)销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形纸片ABCD中,AD=8,AB=6,E是边BC上的点,将纸片沿AE折叠,使点B落在点F处,连接FC,当△EFC为直角三角形时,BE的长为( )
A. 3 B. 5 C. 3或5 D. 3或6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )
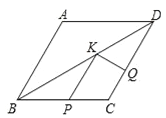
A. 1 B. ![]() C. 2 D.
C. 2 D. ![]() +1
+1
查看答案和解析>>
科目:初中数学 来源: 题型:
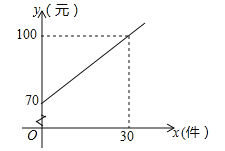
【题目】某快递公司的每位“快递小哥”日收入与每日的派送量成一次函数关系,如图所示.
(1)求每位“快递小哥”的日收入y(元)与日派送量x(件)之间的函数关系式;
(2)已知某“快递小哥”的日收入不少于110元,则他至少要派送多少件?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com