练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

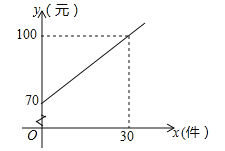
    【题目】某快递公司的每位“快递小哥”日收入与每日的派送量成一次函数关系，如图所示．

    （1）求每位“快递小哥”的日收入y（元）与日派送量x（件）之间的函数关系式；

    （2）已知某“快递小哥”的日收入不少于110元，则他至少要派送多少件？

    【答案】（1）y=x+70；（2）40．

    【解析】

    试题（1）观察函数图象，找出点的坐标，再利用待定系数法求出y与x之间的函数关系式；

    （2）由日收入不少于110元，可得出关于x的一元一次不等式，解之即可得出结论．

    试题解析：解：（1）设每位“快递小哥”的日收入y（元）与日派送量x（件）之间的函数关系式为y=kx+b，将（0，70）、（30，100）代入y=kx+b，得：，解得：，∴每位“快递小哥”的日收入y（元）与日派送量x（件）之间的函数关系式为y=x+70．

    （2）根据题意得：x+70≥110，解得：x≥40．

    答：某“快递小哥”的日收入不少于110元，则他至少要派送40件．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在一条笔直公路BD的正上方A处有一探测仪，AD=24m，∠D=90°，一辆轿车从B点匀速向D点行驶，测得∠ABD=31°，2秒后到达C点，测得∠ACD=50°．

    （Ⅰ）求B，C两点间的距离（结果精确到1m）；

    （Ⅱ）若规定该路段的速度不得超过15m/s，判断此轿车是否超速．

    参考数据：tan31°≈0.6，tan50°≈1.2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某市居民阶梯水价按照月用水量为单位实施，当累计水量达到月阶梯水量分档基数临界点后，即开始实施阶梯加价，分档水量和价格具体如下：

    第一阶梯：户月用水量为0-18吨（含）部分，每吨自来水价格为a元；

    第二阶梯：户月用水量为18-25吨（含）部分，每吨自来水价格为b元；

    第三阶梯：户月用水量为25吨以上的部分，每吨自来水价格为5元.

    （1）已知小蔡家10月用水15吨，水费30元；11月份用水23吨，水费51元，则a= ,b= .

    （2）12月份，小张拜托小蔡帮忙缴纳水费，12月份小蔡家和小张家共缴纳水费111元，已知小蔡家和小张家12月份水量都是整数，且小蔡家本月用水量超过了18吨，则12月份两家各自用水量可能是多少吨？

    （3）某月小蔡家比小王家多交水费28元，小王家比小张家多交水费17元，则三户共交水费多少元？（三户用水量都是整数）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，数轴上的点A、B、C、D、E表示连续的五个整数，对应的数分别为a、b、c、d、e。

    （1）若a＋e＝0，直接写出代数式b＋c＋d的值为_____；

    （2）若a＋b＝7，先化简，再求值：；

    （3）若a＋b＋c＋d＋e＝5，数轴上的点M表示的实数为m，且满足MA＋ME＞12，则m的范围是____。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商场经销一种商品，已知其每件进价为40元。现在每件售价为70元，每星期可卖出500件。该商场通过市场调查发现：若每件涨价1元，则每星期少卖出10件；若每件降价1元，则每星期多卖出m（m为正整数）件。设调查价格后每星期的销售利润为W元。

    （1）设该商品每件涨价x（x为正整数）元，

    ①若x＝5，则每星期可卖出____件，每星期的销售利润为_____元；

    ②当x为何值时，W最大，W的最大值是多少。

    （2）设该商品每件降价y（y为正整数）元，

    ①写出W与Y的函数关系式，并通过计算判断：当m＝10时每星期销售利润能否达到（1）中W的最大值；

    ②若使y＝10时，每星期的销售利润W最大，直接写出W的最大值为_____。

    （3）若每件降价5元时的每星期销售利润，不低于每件涨价15元时的每星期销售利润，求m的取值范围。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了进一步改善环境,郑州市今年增加了绿色自行车的数量,已知A型号的自行车比B型号的自行车的单价低30元,买8辆A型号的自行车与买7辆B型号的自行车所花费用相同.

    (1)A,B两种型号的自行车的单价分别是多少?

    (2)若购买A,B两种自行车共600辆,且A型号自行车的数量不多于B型号自行车的一半,请你给出一种最省钱的方案,并求出该方案所需要的费用.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，EF⊥AD，将平行四边形ABCD沿着EF对折．设∠1的度数为n°，则∠C=______．（用含有n的代数式表示）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC为⊙O的内接三角形，BC=24 , ,点D为弧BC上一动点，CE垂直直线OD于点E, 当点D由B点沿弧BC运动到点C时，点E经过的路径长为（ ）

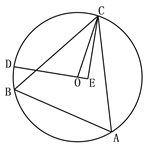
    A. B. C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

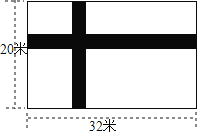
    【题目】如图所示，宽为20米，长为32米的长方形地面上，修筑宽度为x米的两条互相垂直的小路，余下的部分作为耕地，如果要在耕地上铺上草皮，选用草皮的价格是每平米a元，

    （1）求买草皮至少需要多少元？（用含a，x的式子表示）

    （2）计算a＝40，x＝2时，草皮的费用．

    查看答案和解析>>

    同步练习册答案