
【题目】某市居民阶梯水价按照月用水量为单位实施,当累计水量达到月阶梯水量分档基数临界点后,即开始实施阶梯加价,分档水量和价格具体如下:
第一阶梯:户月用水量为0-18吨(含)部分,每吨自来水价格为a元;
第二阶梯:户月用水量为18-25吨(含)部分,每吨自来水价格为b元;
第三阶梯:户月用水量为25吨以上的部分,每吨自来水价格为5元.
(1)已知小蔡家10月用水15吨,水费30元;11月份用水23吨,水费51元,则a= ,b= .
(2)12月份,小张拜托小蔡帮忙缴纳水费,12月份小蔡家和小张家共缴纳水费111元,已知小蔡家和小张家12月份水量都是整数,且小蔡家本月用水量超过了18吨,则12月份两家各自用水量可能是多少吨?
(3)某月小蔡家比小王家多交水费28元,小王家比小张家多交水费17元,则三户共交水费多少元?(三户用水量都是整数)
【答案】(1)2;3;(2)12月份小蔡家和小张家各自用水量可能是19、28吨;24、25吨;25、24吨;28、19吨;29、17吨;31、12吨;33、7吨;35、2吨;(3)128元.
【解析】
(1)由题意可得:第一级的水量为18吨,第二级的水量为23-18=5吨,根据总价等于单价乘以数量就可以求出结论;
(2)由于小蔡家12月份用水量超过18吨,且和小张家共缴纳水费111元,可设小蔡家本月用水x吨,分18<x≤25吨和x>25吨求出小蔡和小张家12月份用水量,根据用水量为整数进行取舍即可;
(3)根据题意可知小蔡家此月水费至少为45元,结合三户用水量都是整数列举出用水量即可求解.
(1)∵15<18,
∴a=30÷15=2元/吨,
∵23>18,
∴b=(51-18×2)÷(23-18)=3元/吨;
(2)设小蔡家12月份用水量为x吨,
①当18<x≤25吨时,小蔡家缴纳的水费为w1=36+3(x-18)=3x-18,小张家缴纳的水费为w2=111-(3x-18)=129-3x,
∵用水量为整数,
∴当x=19吨时,小张家水费为129-57=72元,大于57元,用水量超过25吨,用水量为(72-57)÷5+25=28吨;
同理可求:当x=20吨时,小张家用水量为27![]() 吨(不合题意);
吨(不合题意);
当x=21吨时,小张家用水量为26![]() 吨(不合题意);
吨(不合题意);
当x=22吨时,小张家用水量为26![]() 吨(不合题意);
吨(不合题意);
当x=23吨时,小张家用水量为25![]() 吨(不合题意);
吨(不合题意);
当x=24吨时,小张家用水量为25吨,;
当x=25吨时,小张家24吨;
②当x>25吨时,小蔡家缴纳的水费为w1=57+5(x-25)=5x-68,小张家缴纳的水费为w2=111-(5x-68)=179-5x,
当x=26吨时,小张家水费为49元,用水量为(49-36)÷3+18=22![]() 吨(不合题意);
吨(不合题意);
同理可得,当x=27吨时,小张家用水量为20![]() 吨(不合题意);
吨(不合题意);
当x=28吨时,小张家用水量为19吨;
当x=29吨时,小张家用水量为17吨;
当x=30吨时,小张家用水量为14![]() 吨(不合题意);
吨(不合题意);
当x=31吨时,小张家用水量为12吨;
当x=32吨时,小张家用水量为8![]() 吨(不合题意);
吨(不合题意);
当x=33吨时,小张家用水量为7吨;
当x=34吨时,小张家用水量为4![]() 吨(不合题意);
吨(不合题意);
当x=35吨时,小张家用水量为2吨;
所以,12月份小蔡家和小张家各自用水量可能是19、28吨;24、25吨;25、24吨;28、19吨;29、17吨;31、12吨;33、7吨;35、2吨;
(3)∵小蔡家比小王家多交水费28元,小王家比小张家多交水费17元,
∴小蔡家此月水费至少是45元,
设小蔡家此月用水量为x吨,
当x=21时,小蔡家水费为36+9=45元,小王家水费为17元,小张家水费为0元,由于用水量为整数,故不合题意,
同理可得,当x=22,23,24,25,26时,所求得用水量不为整数;
当x=27时,小蔡家水费为67元,小王家水费为67-28=39元,用水量为(39-36)÷3+18=19吨,小张家水费为39-17=22,用水量为22÷2=11吨(符合题意);
当x=28,29,30,31时,用水量均不满足条件.
所以,三户共交水费为:67+39+22=128(元).


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:
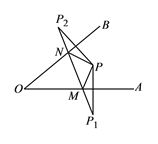
【题目】如图所示,∠A0B=420,点P为∠A0B内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,P1P2=15,则△PMN的周长为________,∠MPN ________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形纸片ABCD中,AD=8,AB=6,E是边BC上的点,将纸片沿AE折叠,使点B落在点F处,连接FC,当△EFC为直角三角形时,BE的长为( )
A. 3 B. 5 C. 3或5 D. 3或6
查看答案和解析>>
科目:初中数学 来源: 题型:
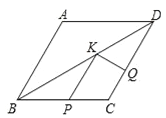
【题目】如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )
A. 1 B. ![]() C. 2 D.
C. 2 D. ![]() +1
+1
查看答案和解析>>
科目:初中数学 来源: 题型:
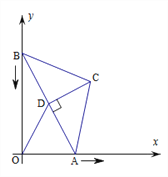
【题目】如图,在△ABC中,BC=AC=5,AB=8,CD为AB边的高,点A在x轴上,点B在y轴上,点C在第一象限,若A从原点出发,沿x轴向右以每秒1个单位长的速度运动,则点B随之沿y轴下滑,并带动△ABC在平面内滑动,设运动时间为t秒,当B到达原点时停止运动
(1)连接OC,线段OC的长随t的变化而变化,当OC最大时,t=____;
(2)当△ABC的边与坐标轴平行时,t=____。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解甲、乙两班英语口语水平,每班随机抽取了10名学生进行了口语测验,测验成绩满分为10分,参加测验的10名学生成绩(单位:分)称为样本数据,抽样调查过程如下:
收集数据
甲、乙两班的样本数据分别为:
甲班:6 7 9 4 6 7 6 9 6 10
乙班:7 8 9 7 5 7 8 5 9 5
整理和描述数据
规定了四个层次:9分以上(含9分)为“优秀”,8-9分(含8分)为“良好”,6-8分(含6分)为“一般”,6分以下(不含6分)为“不合格”。按以上层次分布绘制出如下的扇形统计图。

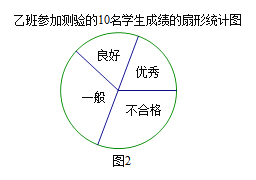
请计算:(1)图1中,“不合格”层次所占的百分比;
(2)图2中,“优秀”层次对应的圆心角的度数。
分析数据
对于甲、乙两班的样本数据,请直接回答:
(1)甲班的平均数是7,中位数是_____;乙班的平均数是_____,中位数是7;
(2)从平均数和中位数看,____班整体成绩更好。
解决问题
若甲班50人,乙班40人,通过计算,估计甲、乙两班“不合格”层次的共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
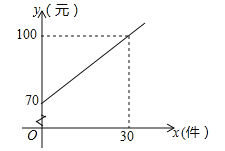
【题目】某快递公司的每位“快递小哥”日收入与每日的派送量成一次函数关系,如图所示.
(1)求每位“快递小哥”的日收入y(元)与日派送量x(件)之间的函数关系式;
(2)已知某“快递小哥”的日收入不少于110元,则他至少要派送多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形OABC中,点A的坐标是(﹣3,1),点B的纵坐标是4,则B,C两点的坐标分别是( )
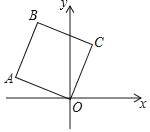
A. (﹣2,4),(1,3) B. (﹣2,4),(2,3)
C. (﹣3,4),(1,4) D. (﹣3,4),(1,3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com